B lớn nhất khi x^2 - 2x + 5 nhỏ nhất.
Ta có: x^2 - 2x + 5 = (x - 1)^2 + 4 >= 4
--> x^2 - 2x + 5 nhỏ nhất bằng 4 (khi x = 1)
--> B lớn nhất bằng 2/4 = 1/2 (khi x = 1)
\(B=\dfrac{2}{x^2-2x+5}\)
Ta có:
\(x^2-2x+5\\ =\left(x^2-2x+4\right)-4+5\\ =\left(x-2\right)^2+1\)
Vì \(\left(x+2\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-2\right)^2+1\ge1\forall x\\ \Rightarrow\dfrac{2}{\left(x-2\right)^2+1}\le2\forall x\\ \Rightarrow B\le2\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\\ \Leftrightarrow x=2\)
Vậy GTLN của B là 2 <=> x =2
giúp em với mn ơi,e đag cần gấp, mn giúp em với ạ
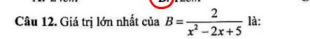
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
giúp em với ạ, em đang vội mong mn giúp đỡ