\(a,\dfrac{a+b-3c}{c}=\dfrac{b+c-3a}{a}=\dfrac{c+a-3b}{b}=\dfrac{-\left(a+b+c\right)}{a+b+c}=-1\\ \Leftrightarrow\left\{{}\begin{matrix}a+b-3c=-c\\b+c-3a=-a\\a+c-3b=-b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b+c=c\\a+b+c=a\\a+b+c=b\end{matrix}\right.\\ \Leftrightarrow a=b=c\)
\(b,\dfrac{a}{2016}=\dfrac{b}{2017}=\dfrac{c}{2018}=\dfrac{a-b}{-1}=\dfrac{b-c}{-1}=\dfrac{c-a}{2}\\ \Leftrightarrow-2\left(a-b\right)=-2\left(b-c\right)=c-a\\ \Leftrightarrow4\left(a-b\right)\left(b-c\right)=4\left(a-b\right)^2=\left[-2\left(a-b\right)\right]^2=\left(c-a\right)^2\\ \Leftrightarrow M=4\left(a-b\right)\left(b-c\right)-\left(c-a\right)^2=\left(c-a\right)^2-\left(c-a\right)^2=0\)
\(c,\dfrac{1}{c}=\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\\ \Leftrightarrow\dfrac{2}{c}=\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{a+b}{ab}\\ \Leftrightarrow ac+bc=2ab\)
Giả sử \(\dfrac{a}{b}=\dfrac{a-c}{c-b}\Leftrightarrow ac-ab=ab-bc\Leftrightarrow ac+bc=2ab\left(\text{luôn đúng}\right)\)
Vậy ta đc đpcm
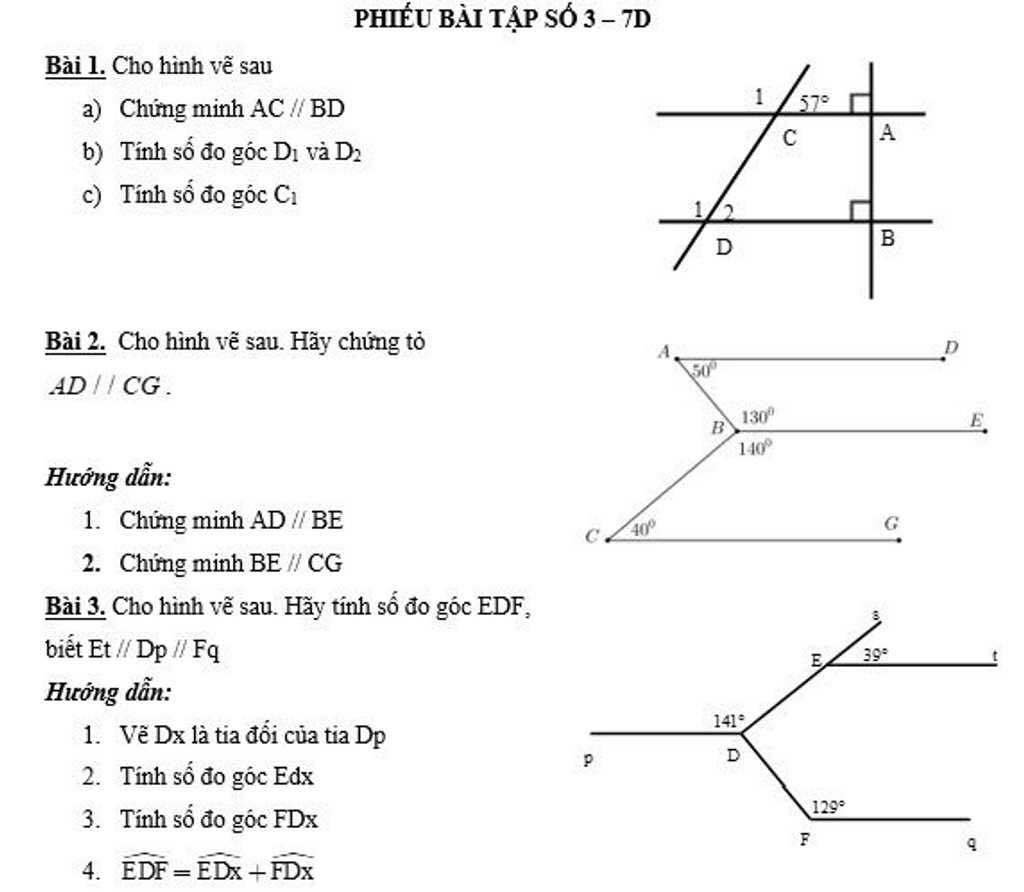Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
