Bài 3.
a) Xét tam giác \(ABM\) và tam giác \(KBM\):
\(BA=BK\) (giả thiết)
\(\widehat{ABM}=\widehat{KBM}\) (vì \(BM\) là tia phân giác của góc \(B\))
\(BM\) cạnh chung
Suy ra \(\Delta ABM=\Delta KBM\) (cạnh - góc - cạnh)
b) Xét tam giác \(BKE\) và tam giác \(BAC\) có:
\(BK=BA\)
\(\widehat{BKE}=\widehat{BAC}\left(=90^o\right)\)
\(\widehat{B}\) chung
Suy ra \(\Delta BKE=\Delta BAC\) (góc - cạnh - góc)
Suy ra \(AC=EK\Leftrightarrow AC-AM=EK-MK\Leftrightarrow MC=ME\)
Do đó tam giác \(MEC\) cân tại \(M\).
c) Tam giác \(BEC\) có \(BE=BC\) nên tam giác \(BEC\) cân mà \(\widehat{B}=60^o\) nên tam giác \(BEC\) đều.
d) \(M\) là giao của hai đường cao \(CA,EK\) của tam giác \(BEC\) nên \(M\) là trực tâm tam giác \(BEC\) mà tam giác \(BEC\) đều nên \(M\) cũng là trọng tâm của tam giác \(BEC\).
Dễ dàng chứng minh được \(\Delta EAH=\Delta ENH\) (góc - cạnh - góc)
suy ra \(\Delta ENM=\Delta EAM\) (cạnh - góc - cạnh).
Suy ra \(EN=EA\) do đó suy ra \(CN=CK\).
Suy ra tam giác \(CNK\) cân tại \(C\) mà \(CA\) là đường phân giác nên nó đồng thời là đường cao do đó \(CA\) vuông góc với \(NK\).






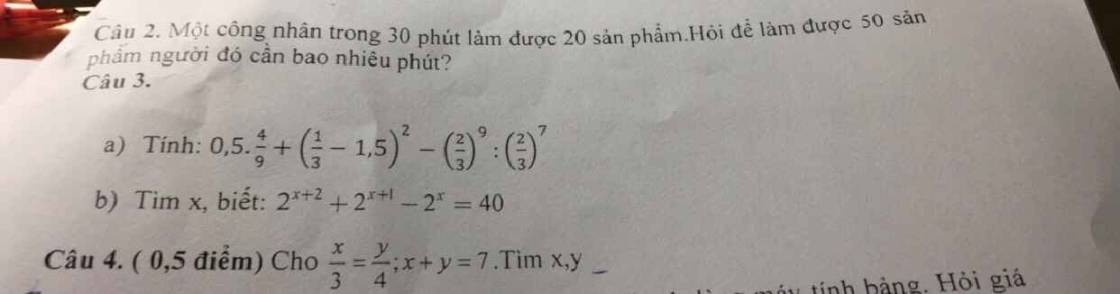 Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...







