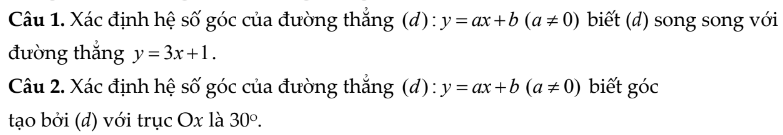19
Từ pt đầu ta có:
\(x^2-xy-2xy+2y^2=0\)
\(\Leftrightarrow x\left(x-y\right)-2y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
TH1: \(x=y\) thế xuống pt dưới:
\(y^2-y-y^2=1\Rightarrow y=-1\Rightarrow x=-1\)
TH2: \(x=2y\) thế xuống pt dưới:
\(\left(2y\right)^2-2y-y^2=1\Leftrightarrow3y^2-2y-1=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-\dfrac{1}{3}\Rightarrow x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(-1;-1\right);\left(1;2\right);\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)\)
21.
Từ pt đầu:
\(xy+2=2x+y\Leftrightarrow xy-y+2-2x=0\)
\(\Leftrightarrow y\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
TH1: \(x=1\) thế xuống pt dưới:
\(2y+y^2+3y=6\Leftrightarrow y^2+5y-6=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-6\end{matrix}\right.\)
TH2: \(y=2\) thế xuông pt dưới
\(4x+4+6=6\Rightarrow x=-1\)
Vậy nghiệm của pt là: \(\left(x;y\right)=\left(1;1\right);\left(1;-6\right);\left(-1;2\right)\)
22.
\(\Leftrightarrow\left\{{}\begin{matrix}9x^2-6xy+y^2+6xy=10\\\left(3x-y\right)\left(10-6xy\right)=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3x-y\right)^2=10-6xy\\\left(3x-y\right)\left(10-6xy\right)=8\end{matrix}\right.\)
Thế \(10-6xy\) từ pt trên xuống dưới ta được
\(\left(3x-y\right)\left(3x-y\right)^2=8\)
\(\Leftrightarrow\left(3x-y\right)^3=2^3\)
\(\Leftrightarrow3x-y=2\)
\(\Leftrightarrow y=3x-2\)
Thế vào pt đầu:
\(9x^2+\left(3x-2\right)^2=10\)
\(\Leftrightarrow18x^2-12x-6=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-\dfrac{1}{3}\Rightarrow y=-3\end{matrix}\right.\)
20.
Từ pt dưới: \(2x+3y=1\Rightarrow3y=1-2x\)
Thế vào pt đầu:
\(x^2+2x.\left(3y\right)=\left(3y\right)^2\)
\(\Leftrightarrow x^2+2x\left(1-2x\right)=\left(1-2x\right)^2\)
\(\Leftrightarrow7x^2-6x+1=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{2}}{7}\\x=\dfrac{3-\sqrt{2}}{7}\end{matrix}\right.\) thế vào \(y=\dfrac{1-2x}{3}\Rightarrow\left[{}\begin{matrix}y=\dfrac{1-2\sqrt{2}}{21}\\y=\dfrac{1+2\sqrt{2}}{21}\end{matrix}\right.\)
Vậy nghiệm của pt là: ...









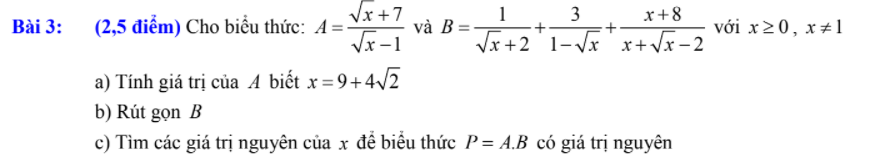 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.