Câu 4:
\(x^2y^2z^2=4\Rightarrow xyz=2\Rightarrow x^3y^3z^3=8\)
\(x^3+y^3-z^3=0\Rightarrow\left[{}\begin{matrix}x^3+y^3=z^3\Rightarrow3x^3+3y^3=3z^3\\y^3-z^3=-x^3\Rightarrow4y^3-4z^3=-4x^3\\x^3-z^3=-y^3\Rightarrow5x^3-5z^3=-5y^3\end{matrix}\right.\)
\(M=\left(3x^3+3y^3\right)\left(4y^3-4z^3\right)\left(5x^3-5z^3\right)=3z^3.\left(-4x^3\right).\left(-5y^3\right)=60.8=480\)

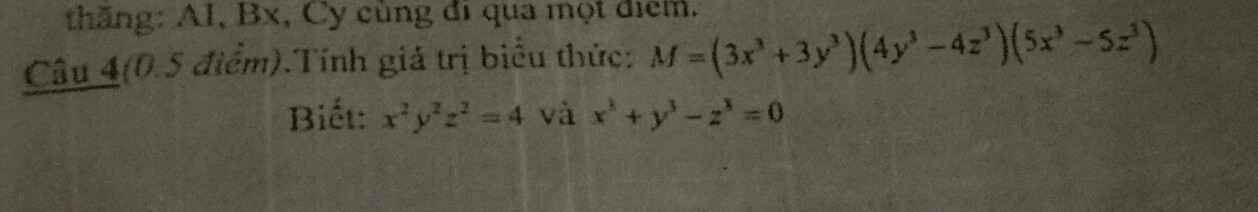






 cac ban giup mik vs aj
cac ban giup mik vs aj










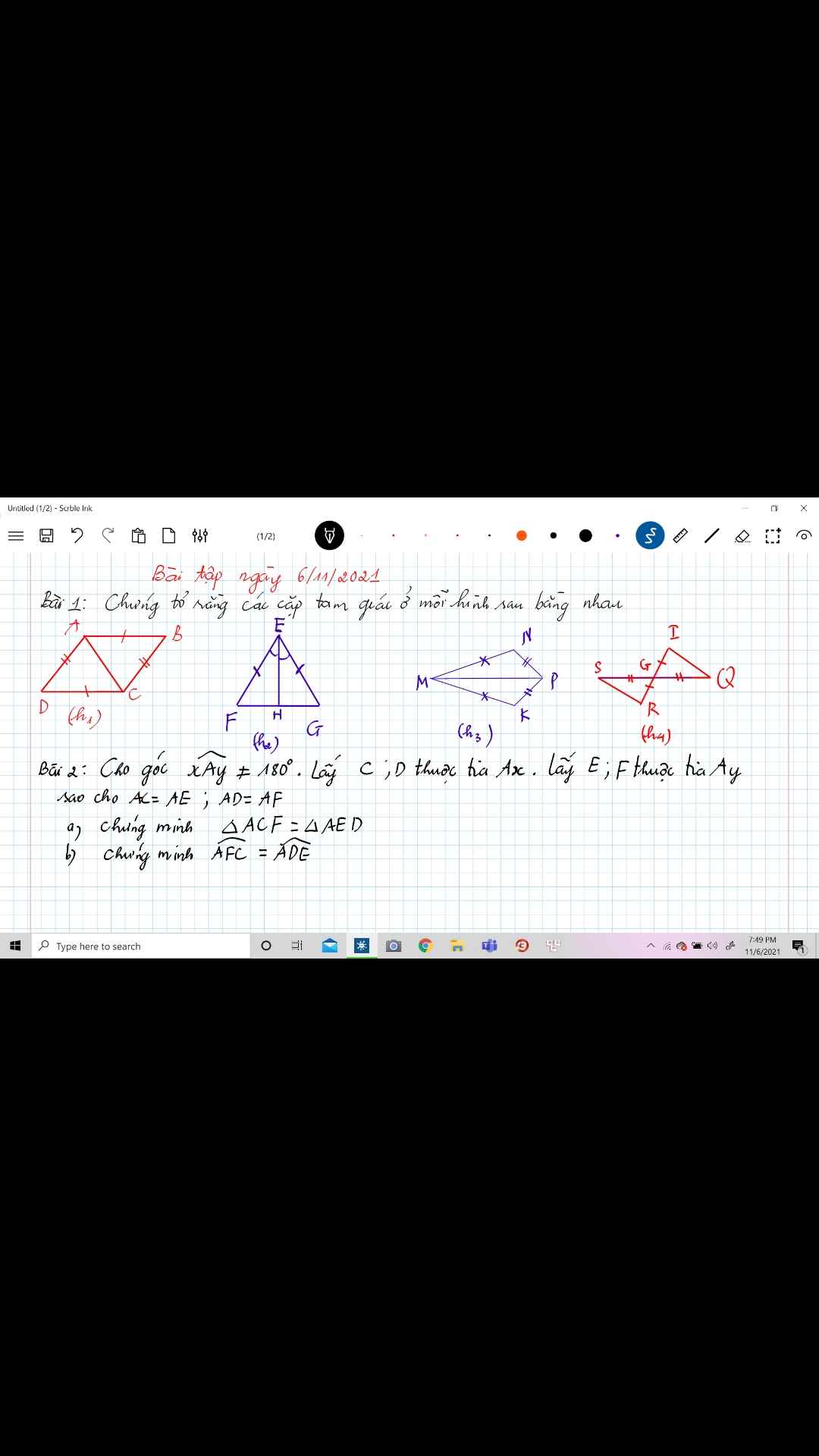


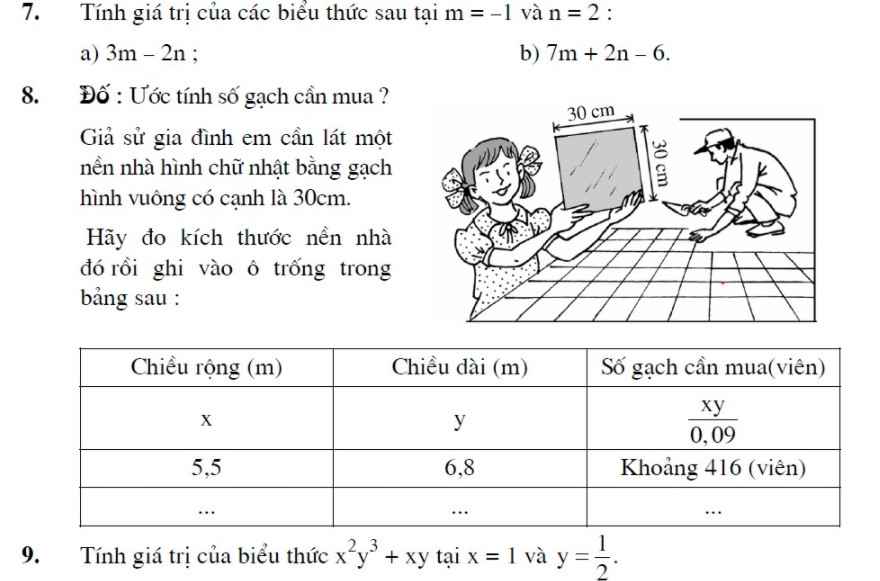 cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik
cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik