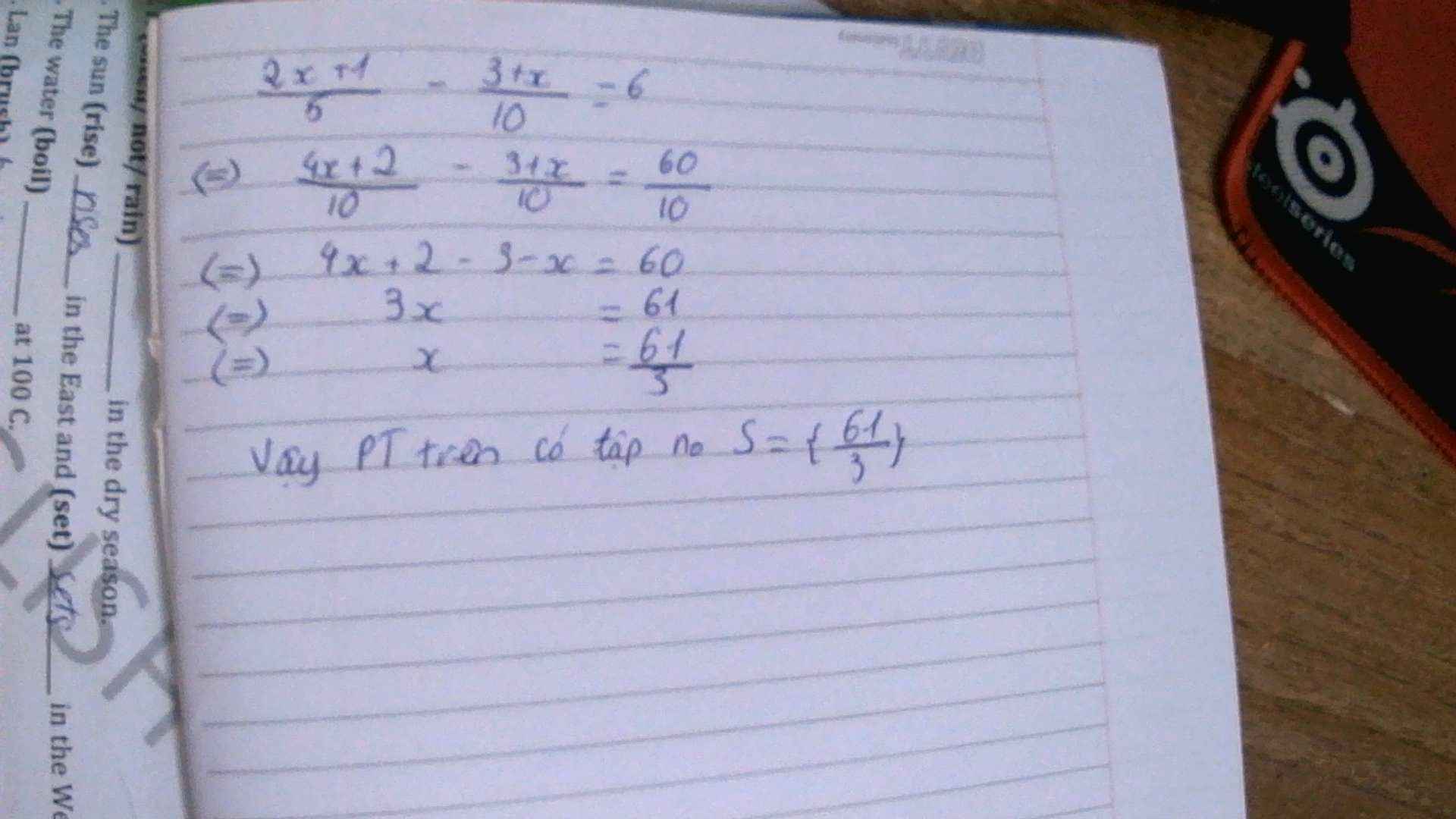a.\(\dfrac{2x+1}{5}-\dfrac{3+x}{10}=6\)
\(\Leftrightarrow\dfrac{2\left(2x+1\right)-\left(3+x\right)}{10}=\dfrac{60}{10}\)
\(\Leftrightarrow2\left(2x+1\right)-\left(3+x\right)=60\)
\(\Leftrightarrow4x+2-3-x=60\)
\(\Leftrightarrow3x=61\)
\(\Leftrightarrow x=\dfrac{61}{3}\)
Vậy \(S=\left\{\dfrac{61}{3}\right\}\)
b.\(\left|x-2\right|=3x+5\)
\(ĐK:x\ge-\dfrac{5}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3x+5\\2-x=3x+5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{7}{2}\left(ktm\right)\\x=-\dfrac{3}{4}\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{3}{4}\right\}\)
\(\dfrac{2x+1}{5}-\dfrac{3+x}{10}=6\)
\(\Leftrightarrow\dfrac{2\left(2x+1\right)}{10}-\dfrac{3+x}{10}=\dfrac{60}{10}\)
\(\Leftrightarrow4x+2-3-x=60\)
\(\Leftrightarrow3x-1=60\)
\(\Leftrightarrow3x=61\)
\(\Leftrightarrow x=\dfrac{61}{3}\)
Vậy....
\(\left|x-2\right|=3x+5\)
Nếu \(x-2\ge0\) thì \(x\ge2\)
\(\Leftrightarrow x-2=3x+5\)
\(\Leftrightarrow x-3x=5+2\)
\(\Leftrightarrow-2x=7\)
\(\Leftrightarrow x=-\dfrac{7}{2}\) (ktm)
Nếu \(x-2< 0\) thì \(x< 2\)
\(\Leftrightarrow x-2=-3x-5\)
\(\Leftrightarrow x+3x=-5+2\)
\(\Leftrightarrow4x=-3\)
\(\Leftrightarrow x=-\dfrac{3}{4}\left(tm\right)\)
Vậy.....

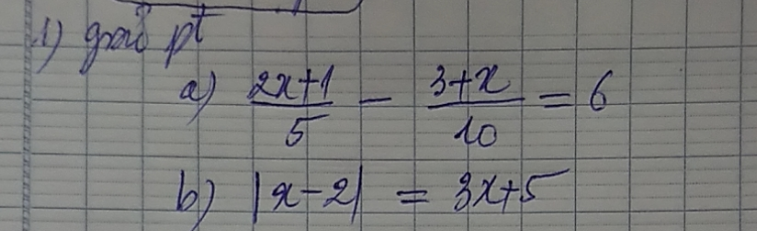 lam gium minh voi a
lam gium minh voi a




![𒅒[̲̅t̲̅]â[̲̅y̲̅]♜[̲̅d̲̅]...](https://hoc24.vn/images/avt/avt6104997_256by256.jpg)