\(2,\\ a,ĐK:x\in R\\ PT\Leftrightarrow\sqrt{\left(3x+1\right)^2}=1-2x\\ \Leftrightarrow\left|3x+1\right|=1-2x\Leftrightarrow\left[{}\begin{matrix}3x+1=1-2x\left(x\ge-\dfrac{1}{3}\right)\\3x+1=2x-1\left(x< -\dfrac{1}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\\ b,ĐK:x\ge4\\ PT\Leftrightarrow6\cdot\dfrac{1}{3}\sqrt{x-4}+\dfrac{2}{5}\cdot5\sqrt{x-4}=2\sqrt{x-4}+10\\ \Leftrightarrow2\sqrt{x-4}=10\Leftrightarrow\sqrt{x-4}=5\\ \Leftrightarrow x-4=25\Leftrightarrow x=29\left(tm\right)\)
Đúng 3
Bình luận (0)
Các câu hỏi tương tự
Làm giùm mình bài này nha
Chứng minh:
2√(2 + √3 ) = √2 + √6
Làm giùm mình bài này
|x1 - x2| = 5
https://photos.app.goo.gl/Gog7BMLzzGX8nyJU7 Làm giúp mình với làm hết giùm mình đi huhu
 Làm giùm bài 7
Làm giùm bài 7
Giải bài này giùm mình với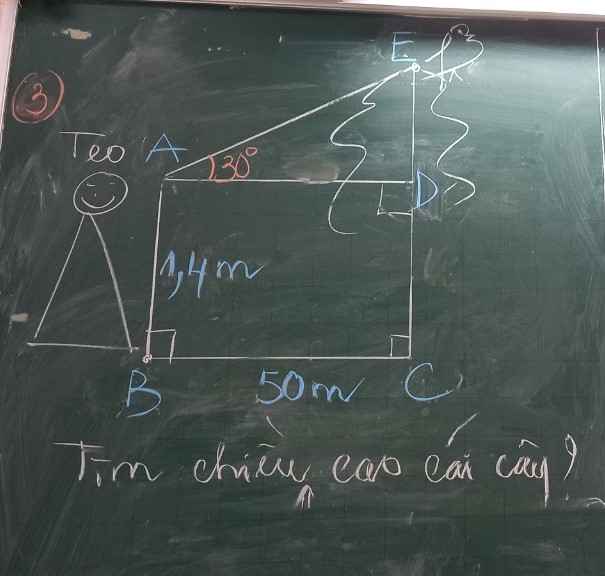
Tìm X;Y,biết
\(5X^2-3XY+X+Y-Y^2=0\)
LÀM GIÙM MÌNH VỚI MÌNH CẢM ƠN BẠN NHIỀU !

chú ý chỉ làm giùm mk ý b bài 4 thôi nha
Cái bài mik mới gửi làm với giải thích giùm mik lun i
mọi người giải giùm mình bài này với
\(x^2-8x+10=\left(x+2\right)\sqrt{2x-1}\)














