Bài 5:
a.
$D=\frac{2m+3}{3m-1}$
$\Rightarrow 3D=\frac{6m+9}{3m-1}=\frac{2(3m-1)+11}{3m-1}=2+\frac{11}{3m-1}$
Để $D$ lớn nhất thì $\frac{11}{3m-1}$ lớn nhất
$\Rightarrow 3m-1$ là số dương nhỏ nhất
Với $m\in\mathbb{N}^*(m\geq 1)$ thì $3m-1$ nhận giá trị dương nhỏ nhất khi $m=1$
b.
Để $D$ là số tự nhiên thì $3D=2+\frac{11}{3m-1}$ là số tự nhiên chia hết cho $3$
Trước hết $\frac{11}{3m-1}\in\mathbb{Z}$
$\Rightarrow 3m-1\in\left\{1; -1; 11;-11\right\}$
$\Rightarrow m\in\left\{0; 4\right\}$ (do $m$ tự nhiên)
Thay vào biểu thức $D$ ban đầu thì $m=4$ thỏa mãn.







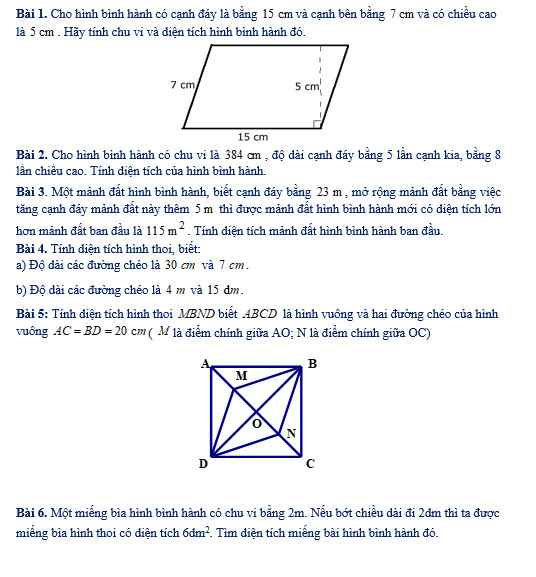 làm bài 3 4 5 6 thôi mn nha chậm nhất là 9h30 ạ
làm bài 3 4 5 6 thôi mn nha chậm nhất là 9h30 ạ 
 đúng mik tick bài 90 nhe làm mỗi bài 90 thôi dành cho 5 bạn nhanh nhất giải thưởng to nhe
đúng mik tick bài 90 nhe làm mỗi bài 90 thôi dành cho 5 bạn nhanh nhất giải thưởng to nhe

 làm bài 6 thôi
làm bài 6 thôi

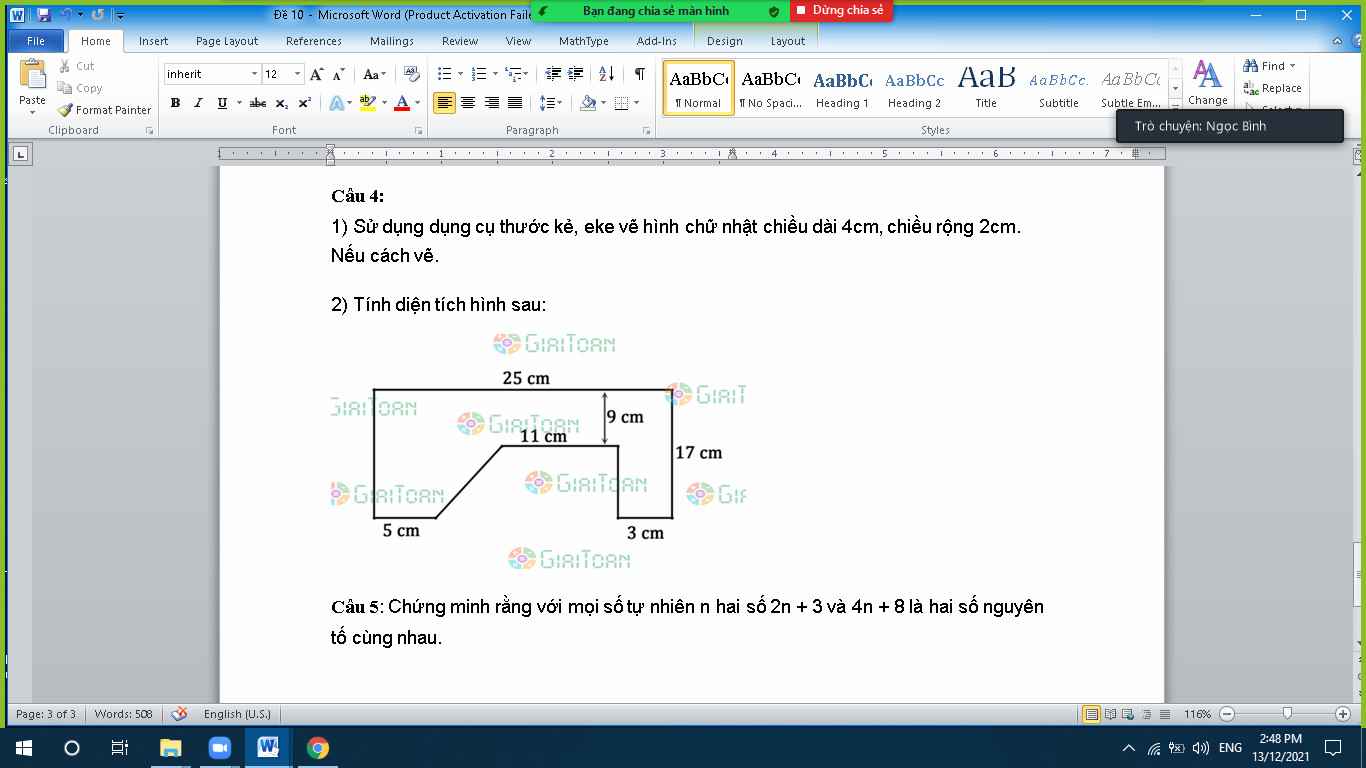



 làm giúp mik đúng tick 3 lần làm mỗi bài 3 thôi trình bày từ đầu đến cuối làm mỗi bài 3 thôi nhiều bn nhìn thấy nhiều bỏ qua luôn mà chưa đọc mong các bn giúp
làm giúp mik đúng tick 3 lần làm mỗi bài 3 thôi trình bày từ đầu đến cuối làm mỗi bài 3 thôi nhiều bn nhìn thấy nhiều bỏ qua luôn mà chưa đọc mong các bn giúp