Câu 4:
Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(A=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)
ta có b1=a1(=60)(1)
mà 2 góc này ở vị trí so le trong(2)
nên BC //AD
ta có d1+c2=180(trong cùng phía)
Câu 3
a) Ta có: \(\widehat{B_1}=\widehat{A_1}=60^0\)
Mà 2 góc này so le trong
=> BC//AD
b) Ta có: BC//AD(cmt)
\(\Rightarrow\widehat{D_1}+\widehat{C_2}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{C_2}=180^0-80^0=100^0\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}=100^0\)(đối đỉnh)

 Làm bài 3 nha.
Làm bài 3 nha.













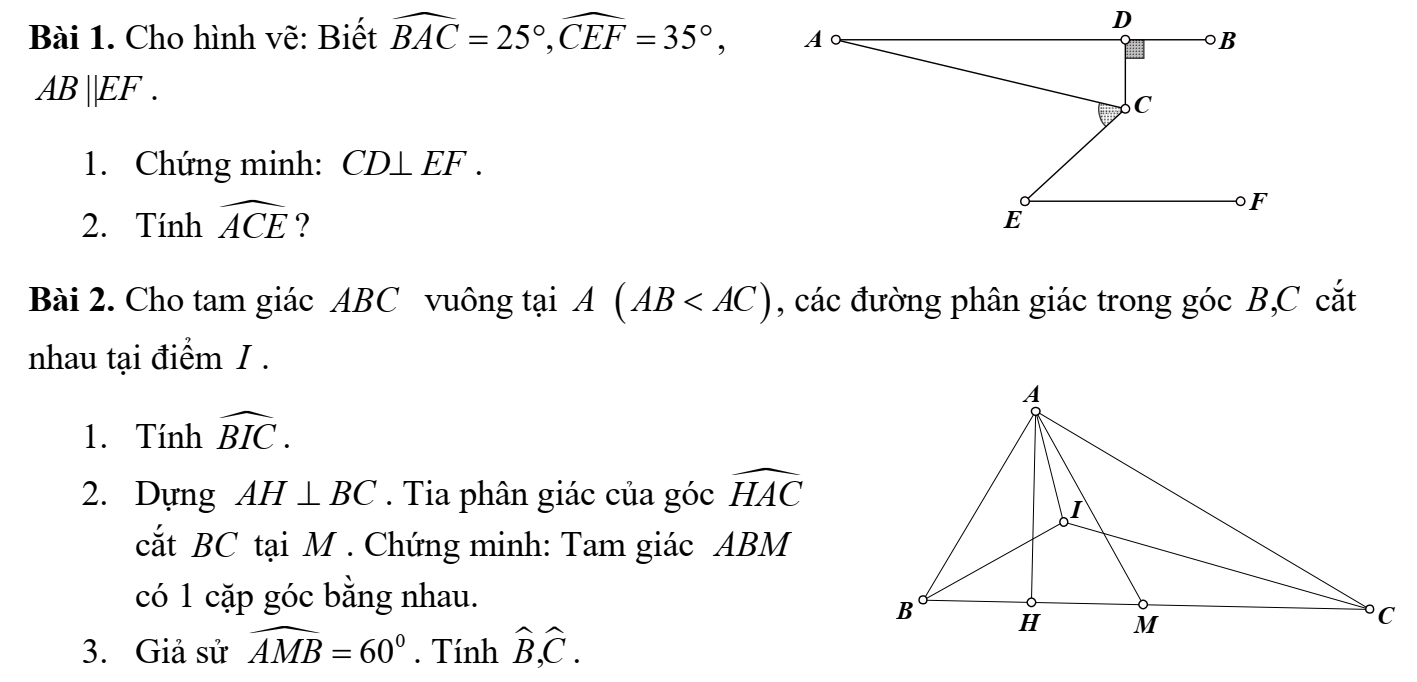
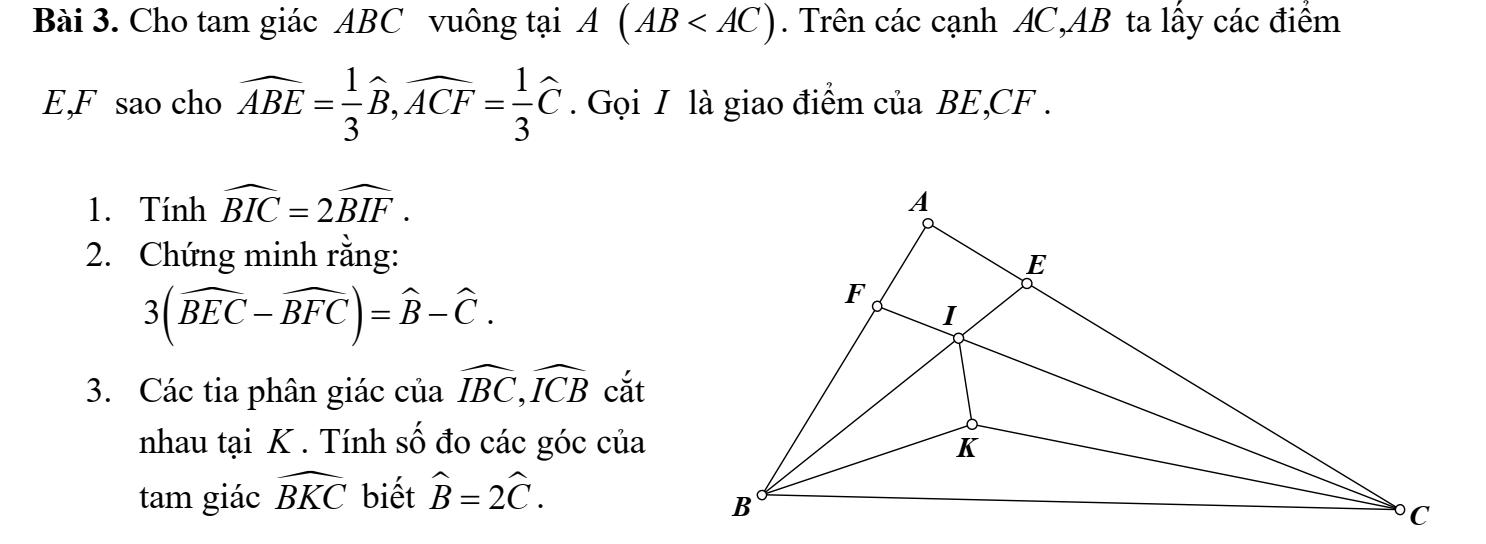


 làm hộ mình bài 5,1,2,3,4 nha
làm hộ mình bài 5,1,2,3,4 nha