Các câu hỏi tương tự
Kí hiệu
C
n
k
là số tổ hợp chập k của n phần tử (0
≤
k
≤
n). Mệnh đề nào sau đây đúng?
A
.
C
n
k
n
!
(
n
-
k
)
!...
Đọc tiếp
Kí hiệu C n k là số tổ hợp chập k của n phần tử (0 ≤ k ≤ n). Mệnh đề nào sau đây đúng?
A . C n k = n ! ( n - k ) !
B . C n k = n ! k !
C . C n k = n ! k ! ( n - k ) !
D . C n k = n ! k ! ( n - k ) !
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} n thì a b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} 1 thì a b”Mệnh đề A(1) đúng vì max{a,b} 1 và a,b là những số nguyên dương thì a b 1.Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1Bước 3: xét max{a,b} k+1 ⇒max{a-1,b-1} k+ 1-1 kDo a(k) là mệnh đề đúng nên a- 1 b-1 ⇒ a b⇒...
Đọc tiếp
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n
∈
ℕ
*
,
k
≤
n
).
A
.
k
!
(
k
-
n
)
!
B
.
C
n...
Đọc tiếp
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n ∈ ℕ * , k ≤ n ).
A . k ! ( k - n ) !
B . C n k . k ! .
C . C n k . ( n - k ) ! .
D . k ! ( n - k ) ! n !
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử
1
≤
k
≤
n
Đọc tiếp
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử 1 ≤ k ≤ n
![]()
![]()
![]()
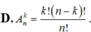
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k
...
Đọc tiếp
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A . C n k = n ! ( n - k ) !
B . C n k = n ! k ! ( n - k ) !
C . A n k = n ! ( n - k ) !
D . A n k = n ! k ! ( n - k ) !
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phần tử và một tổ hợp chập k của n phần tử.
Cho k, n (k n) là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
A
.
A
n
k
n
!
k
!
B
.
A
n
k
k
!
C
n
k...
Đọc tiếp
Cho k, n (k < n) là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
A . A n k = n ! k !
B . A n k = k ! C n k
C . A n k = n ! k ! ( n - k ) !
D . A n k = n ! C n k
Số các tổ hợp chập k của một tập hợp có n phần tử 1
≤
k
≤
n là :
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k...
Đọc tiếp
Số các tổ hợp chập k của một tập hợp có n phần tử 1 ≤ k ≤ n là :
A . C n k = n ! ( n - k ) !
B . C n k = A n k k !
C . C n k = A n k ( n - k ) !
D . C n k = k ! ( n - k ) ! n !



