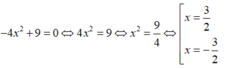Các câu hỏi tương tự
Không dùng công thức nghiệm, tìm số nghiệm của phương trình − 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Không dùng công thức nghiệm, tìm số nghiệm của phương trình - 4 x 2 + 9 = 0
A. 0
B. 1
C. 3
D. 2
Không dùng công thức nghiệm, tìm số nghiệm của phương trình − 9 x 2 + 30 x − 25 = 0
A. 0
B. 1
C. 3
D. 2
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm...
Đọc tiếp
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4= 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 = 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 = 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm kép dương. e) Có một nghiệm bằng 0 và một nghiệm dương.
Cho phương trình x2 + 2(2m-1)x + 3(m2 - 1) = 0 (m là tham số)
a) Với giá trị nào của tham số m thì phương trình có nghiệm?
b) Trong trường hợp phương trình có hai nghiệm x1 và x2, dùng hệ thức Vi-ét, hãy tìm hệ thức liên hệ giữa hai nghiệm x1 và x2 của phương trình không phụ thuộc vào m.
BÀI1. Cho phương trình : mx^2-left(2m+3right)x+m-40a) Tìm m để phương trình có hai nghiệm phân biệt x1, x2.b) Tìm hệ thức liên hệ giữa hai nghiệm x1, x2 không phụ thuộc m.BÀI2. Cho phương trình : left(m-1right)x^2-2mx+m+10a) Chứng minh phương trình luôn có 2 nghiệm phân biệt x1,x2b) Xác định m để phương trình có 2 nghiệm bằng 5. Từ đó tính tổng 2 nghiệm của phương trình.c) Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc x.
Đọc tiếp
BÀI1. Cho phương trình : \(mx^2-\left(2m+3\right)x+m-4=0\)
a) Tìm m để phương trình có hai nghiệm phân biệt x1, x2.
b) Tìm hệ thức liên hệ giữa hai nghiệm x1, x2 không phụ thuộc m.
BÀI2. Cho phương trình : \(\left(m-1\right)x^2-2mx+m+1=0\)
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt x1,x2
b) Xác định m để phương trình có 2 nghiệm bằng 5. Từ đó tính tổng 2 nghiệm của phương trình.
c) Tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc x.
Không dùng công thức nghiệm, tính tích các nghiệm của phương trình 3 x 2 – 10 x + 3 = 0
A. 3
B. 10 3
C. 1
D. -1
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
Nêu điều kiện để phương trình
a
x
2
+
b
x
+
c
0
(a ≠...
Đọc tiếp
3. Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai
a x 2 + b x + c = 0 ( a ≠ 0 )
Nêu điều kiện để phương trình a x 2 + b x + c = 0 (a ≠ 0) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
1954 x 2 + 21 x – 1975 = 0
Nêu điều kiện để phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình
2005 x 2 + 104 x – 1901 = 0
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a
)
2
x
2
−
7
x
+
3
0
b
)
6
x
2
+...
Đọc tiếp
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
a ) 2 x 2 − 7 x + 3 = 0 b ) 6 x 2 + x + 5 = 0 c ) 6 x 2 + x − 5 = 0 d ) 3 x 2 + 5 x + 2 = 0 e ) y 2 − 8 y + 16 = 0 f ) 16 z 2 + 24 z + 9 = 0