Đáp án D
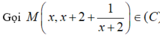
Khoảng cách từ M đến d là h(M;d) cho bởi
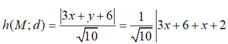
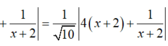
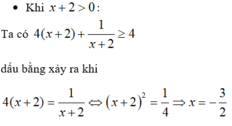

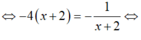
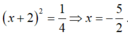

Đáp án D
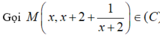
Khoảng cách từ M đến d là h(M;d) cho bởi
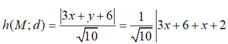
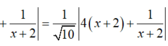
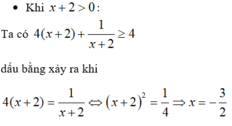

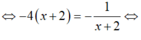
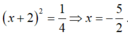

Tổng khoảng cách từ một điểm thuộc đồ thị hàm số y = x + 3 x - 3 (C) đến 2 đường tiệm cận của lớn hơn hoặc bằng
A. ![]() .
.
B. ![]() .
.
C. 6.
D. 12.
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Tọa độ điểm M có hoành độ nguyên thuộc đồ thị (C) của hàm số y = x + 2 x - 1 có khoảng cách đến đường thẳng
d: x - y +1 = 0 bằng 1 2 là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = 2 x + 3 x + 1 có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d1: 3x+ 4y-2=0 bằng 2.
A. 2.
B. 3.
C. 4.
D. 0.
Cho hàm số y = 2 x + 3 x + 1 có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d1: 3x+4y-2=0 bằng 2.
A. 2.
B. 3.
C. 4.
D. 0.
Cho hàm số y = x 2 + 3 x + 3 x + 2 có đồ thị (C). Tổng khoảng cách từ một điểm M thuộc (C) đến hai hai trục tọa độ đạt giá trị nhỏ nhất bằng ?
A.1B. 1 2 C.2D. 3 2
B. 1 2
C.2
D. 3 2
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Tổng khoảng cách từ một điểm M thuộc (C) đến hai tiệm cận của (C) đạt giá trị nhỏ nhất
bằng
A. 3.
B. 4.
C. 2 2
D. 2
Tọa độ tất cả các điểm thuộc đồ thị (C) của hàm số y = x + 1 x - 2 sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất là
A. (1;1)
B.![]()
C. ![]()
D. ![]()