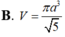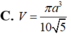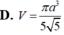Khối chóp C.BDNM có CB là đường cao nên có thể tích ![]() trong đó
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
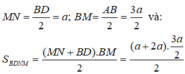
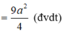
Thể tích của khối chóp C.BDNM là:
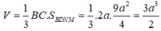
Khối chóp C.BDNM có CB là đường cao nên có thể tích ![]() trong đó
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
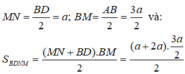
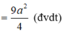
Thể tích của khối chóp C.BDNM là:
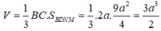
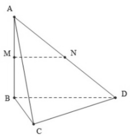
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = 3a, BC =BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
A. V = 8 a 3
B. V = 2 a 3 3
C. V = 9 a 3 4
D. V = a 3
Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB=3a, AC=6a, AD=4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
![]()
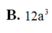
![]()
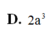
Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3cm, AC = 6cm, AD = 4cm. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có AC = 3a, B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
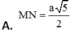
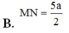
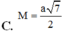
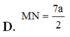
Cho tứ diện ABCD có A C = 3 a , B D = 4 a . Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.
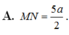
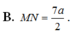
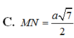

Bài 1: cho hình chóp S.ABCD có đáy ABCD là hình thang , BAD=ABC= 90 độ. Cạnh AB=BC=a, AD=2a, SA vuông góc ( ABCD ), Sa=2a. Gọi M,N lần lượt là trung điểm của SA và SD. Tính theo a thể tích khối chóp S.BCNM
Bài 2: cho hình chóp tứ giác đều S.ABCD có AB = a; SA = a\(\sqrt{2}\) . Gọi M,N lần lượt là trung điểm của SA,SB,SD. Tính theo a thể tích của khối tứ diện A.MNP
Cho khối tứ diện đều ABCD có thể tích là V. Gọi M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối chóp AMNPQ là:
A. V 6
B. V 3
C. V 4
D. V 2 3
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, AB = 6a, AC = 5a, AD = 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
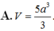
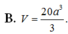
![]()
![]()
Cho hình chóp S.BCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC; A D = 3 B C = 3 a ; A B = a ; S A = a 3 . Điểm I thỏa mãn A D → = 3 A I → . M là trung điểm SD, H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).