Chọn A.
Ta có: a 2 = 16 b 2 = 9 c 2 = a 2 + b 2 ⇒ a = 5 b = 3 c = 5
Các tiêu điểm là F1( -5;0) và F2(5;0).
Chọn A.
Ta có: a 2 = 16 b 2 = 9 c 2 = a 2 + b 2 ⇒ a = 5 b = 3 c = 5
Các tiêu điểm là F1( -5;0) và F2(5;0).
Hypebol có hai tiêu điểm là F1(-2;0) và F2 (2;0) và một đỉnh A(1;0) có phương trình là chính tắc là
A. 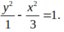
B. 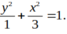
C. 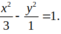
D. 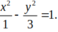
Cho Elip có các tiêu điểm F1(-4;0) và F2(4;0) và một điểm M nằm trên (E) biết rằng chu vi của tam giác MF1F2 bằng 18. Lúc đó tâm sai của (E) là:
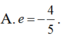
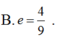
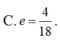
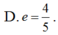
Trong mặt phẳng Oxy, cho hai điểm F1(-4; 0) và F2(4;0) và điểm A(0; 3). Điểm M thuộc E nào sau đây thỏa MF1= 3MF2.
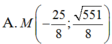
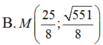
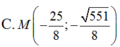
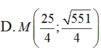
Elip x2/16+y2/9=1 có hai tiêu điểm F1, F2; M là một điểm bất kì nằm trên elip. Tính MF1+MF2 A.10. B.8 C.6 D.12
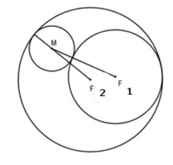
Cho hai đường tròn C1(F1,R1) và C2(F2,R2) . C1 nằm trong C2 và F1 ≠ F2 . Đường tròn C thay đổi luôn tiếp xúc ngoài với C1 và tiếp xúc trong với C2. Hãy chứng tỏ rằng tâm M của đường tròn C di động trên một elip.
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
Viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
viết phương trình chính tắc của elip đi qua điểm A(0;-4) và có 1 tiêu điểm F2(3;0)
Biết Elip (E) có các tiêu điểm F 1 ( - 7 ; 0 ) , F 2 ( 7 ; 0 ) và đi qua M - 7 ; 9 4 Gọi N là điểm đối xứng với M qua gốc toạ độ. Chọn khẳng định đúng?
A. x 2 16 + y 2 12 = 1
B . M( 2;3)
C. F1( -2;0) và F2( 2;0)
D.NF1+ MF1= 8.
Cho elip (E) có phương trình x 2 169 + y 2 25 = 1 với hai tiêu điểm là F 1 , F 2 . Với điểm M bất kì trên (E) thì chu vi tam giác M F 1 F 2 là:
A. 50
B. 36
C. 34
D. Thay đổi phụ thuộc vào vị trí M