Chọn A
Dựa vào đồ thị của hàm số ![]() , đồ thị đi qua các điểm
, đồ thị đi qua các điểm ![]()
Ta có hệ phương trình
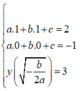
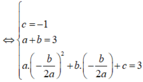
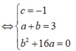
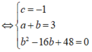
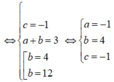
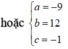
Suy ra M = a 2 + b 2 + c 2 hoặc M = a 2 + b 2 + c 2 = 226. Từ đó M có thể nhận giá trị là 18.
Chọn A
Dựa vào đồ thị của hàm số ![]() , đồ thị đi qua các điểm
, đồ thị đi qua các điểm ![]()
Ta có hệ phương trình
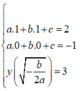
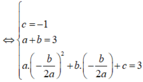
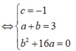
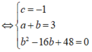
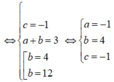
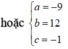
Suy ra M = a 2 + b 2 + c 2 hoặc M = a 2 + b 2 + c 2 = 226. Từ đó M có thể nhận giá trị là 18.
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 Đường thẳng d:y=x+m cắt đồ thị (C) tại hai điểm A, B phân biệt và A B = 2 2 khi m nhận giá trị nào trong các giá trị nào sau đây?
A. m = 1
B. m = 5
C. m = -2
D. m = 8
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
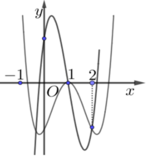
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
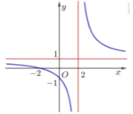
A. - 2
B. -3
C. - 4
D. -5
Hình vẽ bên là đồ thị C của hàm số y = f x .
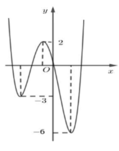
Giả sử m là tham số thực nhận giá trị thuộc nửa khoảng ( 0 ; 3 ] . Hỏi hàm số y = f x - 1 + m có thể có bao nhiêu điểm cực trị
A. 5 hoặc 7 điểm
B. 3 điểm
C. 6 hoặc 8 điểm
D. 4 điểm
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d với a, b, c, d là các số thực, có đồ thị như hình bên.
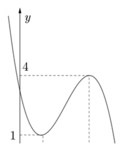
Có bao nhiêu giá trị nguyên của tham số m để phương trình f e x 2 = m có ba nghiệm phân biệt?
A. Vô số.
B. 3.
C. 1.
D. 2.
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số y = a x 3 + b x 2 + c x + d ; với a, b, c, d là các số thực, có đồ thị như hình vẽ bên:
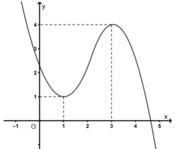
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 x 2 = m có đúng 3 nghiệm thực phân biệt ?
A. 1
B. 2
C. 3
D. Vô số.