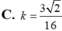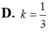Các câu hỏi tương tự
Một mặt phẳng chứa trục hình trụ, cắt hình trụ đó theo thiết diện là một hình vuông cạnh a. Tính thể tích V của hình trụ đó.
Đọc tiếp
Một mặt phẳng chứa trục hình trụ, cắt hình trụ đó theo thiết diện là một hình vuông cạnh a. Tính thể tích V của hình trụ đó.
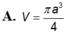
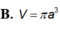
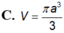
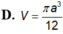
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng
a
2
. Tính thể tích V của khối trụ (T).
Đọc tiếp
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng a 2 . Tính thể tích V của khối trụ (T).
![]()
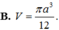
![]()
![]()
Cho hình trụ có bán kính đáy bằng
a
2
. Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng
a
2
ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
Đọc tiếp
Cho hình trụ có bán kính đáy bằng a 2 . Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng a 2 ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
![]()
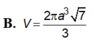
![]()
![]()
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
36
πa
2
. Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
Đọc tiếp
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36 πa 2 . Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
![]()
![]()
![]()
![]()
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
36
πa
2
. Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ
Đọc tiếp
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36 πa 2 . Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ
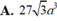
![]()
![]()
![]()
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng
36
πa
2
. Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
Đọc tiếp
Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng 36 πa 2 . Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
![]()
![]()
![]()
![]()
Cho hình trụ nội tiếp mặt cầu thảo mãn chiều cao của trụ băng bán kính mặt cầu. gọi
V
t
,
V
c
lần lượt là thể tích của hình trụ và hình cầu. Khi đó tỉ số thể tích
V
t
V
c
bằng A. ...
Đọc tiếp
Cho hình trụ nội tiếp mặt cầu thảo mãn chiều cao của trụ băng bán kính mặt cầu. gọi V t , V c lần lượt là thể tích của hình trụ và hình cầu. Khi đó tỉ số thể tích V t V c bằng

A. 1 4
B. 4 9
C. 3 4
D. 9 16
Cho hình trụ nội tiếp mặt cầu thỏa mãn chiều cao của trụ bằng bán kính mặt cầu. Gọi Vt , Vc lần lượt là thể tích của hình trụ và hình cầu. Khi đó tỉ số thể tích
V
t
V
c
bằng
Đọc tiếp
Cho hình trụ nội tiếp mặt cầu thỏa mãn chiều cao của trụ
bằng bán kính mặt cầu. Gọi Vt , Vc lần lượt là thể tích của
hình trụ và hình cầu. Khi đó tỉ số thể tích V t V c bằng
![]()
![]()
![]()
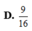
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng
a
2
. Tính thể tích của khối trụ (T).
Đọc tiếp
Khi cắt khối trụ (T) bởi một mặt phẳng qua trục của nó ta được thiết diện là một hình vuông có diện tích bằng a 2 . Tính thể tích của khối trụ (T).
![]()
![]()
![]()
![]()