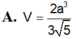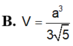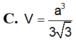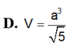Các câu hỏi tương tự
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60. Tính thể tích V của hình chóp S.ABCD. A)a³✓3/2 B)a³✓3/6 C)a³✓3/12 D)a³✓3/24
Hình chóp S.ABC có SA a, SB a
5
, SC a
3
,
A
S
B
^
B
S
C
^
60
°
. Tính khoảng cách h từ A tới mp(SBC). A. h a
2
3
B. ...
Đọc tiếp
Hình chóp S.ABC có SA = a, SB = a 5 , SC = a 3 , A S B ^ = B S C ^ = 60 ° . Tính khoảng cách h từ A tới mp(SBC).
A. h = a 2 3
B. a 3 2
C. a 5 2
D. a 2
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB a, BC a
6
, khoảng cách từ A đến mặt (SCD) bằng
6
a/3 A.
V
6
6
a
3
B.
V
2
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = a 6 , khoảng cách từ A đến mặt (SCD) bằng 6 a/3
A. V = 6 6 a 3
B. V = 2 4 a 3
C. V = 2 2 a 3
D. V = 2 6 a 3
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC a
3
, AD 2a, AB a
5
. Tính thể tích V của hình hộp. A. V
2
a
3
15
B. V
a
3
15
3
C. V
a
3
6
D. V
3
a...
Đọc tiếp
Hình hộp chữ nhật ABCD.A’B’C’D’ có AC = a 3 , AD' = 2a, AB' = a 5 . Tính thể tích V của hình hộp.
A. V = 2 a 3 15
B. V = a 3 15 3
C. V = a 3 6
D. V = 3 a 3
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng
3
a/4. Thể tích của hình chóp S.ABC là: A.
V
3
8
a
3
B.
V
2
12
a
3...
Đọc tiếp
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3 a/4. Thể tích của hình chóp S.ABC là:
A. V = 3 8 a 3
B. V = 2 12 a 3
C. V = 3 12 a 3
D. V = 3 24 a 3
Cho
d
1
,
d
2
chéo nhau và khoảng cách
d
1
,
d
2
3
. Biết
d
1
∥
v
1
→...
Đọc tiếp
Cho d 1 , d 2 chéo nhau và khoảng cách d 1 , d 2 = 3 . Biết d 1 ∥ v 1 → = 2 ; - 1 ; 1 ; d 1 ∥ v 2 → = 1 ; 1 ; 2 ; A , B ∈ d 1 và C , D ∈ d 2 sao cho A B = C D = 2 . Biết tứ diện ABCD có thể tích V không phụ thuộc việc chọn các điểm A, B, C, D. Tính V.
![]()
![]()
![]()
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn ABa, ACa
3
. Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Tính thể tích V của khối chóp đã cho
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn AB=a, AC=a 3 . Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Tính thể tích V của khối chóp đã cho