Ta có
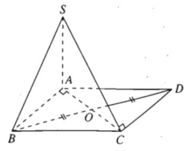
SA ⊥ (ABC) ⇒ SA ⊥ DC ⊂ (ABC)
Vì AC và BD cắt nhau tại trung điểm Ocủa mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có AB // CD. Vì AB ⊥ AC nên CD ⊥ CA. Mặt khác ta có CD ⊥ SA, do đó CD⊥(SCA)

Ta có
SA ⊥ (ABC) ⇒ SA ⊥ DC ⊂ (ABC)
Vì AC và BD cắt nhau tại trung điểm Ocủa mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có AB // CD. Vì AB ⊥ AC nên CD ⊥ CA. Mặt khác ta có CD ⊥ SA, do đó CD⊥(SCA)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết 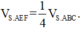 Tính thể tích V của khối chóp S.ABC
Tính thể tích V của khối chóp S.ABC
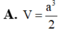
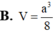
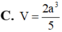
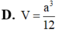
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại với AB = a, BC = 2a.
Điểm H thuộc cạnh AC sao cho CH = 1 3 CA, SH là đường cao hình chóp S.ABC và SH = a 6 3 . Gọi I là trung điểm BC. Tính diện tích thiết diện của hình chóp S.ABC với mặt phẳng đi qua H và vuông góc với AI
A . 2 2 a 2 3
B . 2 a 2 6
C . 3 a 2 3
D . 3 a 2 6
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Mặt phẳng (P) đi qua trung điểm M của AB và vuông góc với SB, cắt AC, SC, SB lần lượt tại N, P, Q. Tứ giác M PQ là hình gì?
A. Hình thang vuông.
B. Hình chữ nhật.
C. Hình thang cân.
D. Hình bình hành.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o . Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
A. d = a 39 13
B. d = a 2
C. d = a
D. d = a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, cạnh bên SA vuông góc với đáy và SA = a 2 . Gọi M là trung điểm của AB. Tính khoảng cách d giữa hai đường thẳng SM và BC
A . d = a 3 2
B . d = a 2 3
C . d = a 3 3
D . d = a 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm S lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác là SBC tam giác đều. Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABC)
A . 90 0
B . 60 0
C . 30 0
D . 45 0
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)
tại H. Chứng minh rằng
a) OA⊥BC,OB⊥AC,OC⊥AB
b) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BC
c) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giác
ABC.
d)
Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minh
rằng các mặt bên của hình chóp là các tam giác vuông.
Bài 8. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D với AD=DC=AB/2 . Gọi I là trung điểm của đoạn AB, SA vuông góc với mặt đáy. Chứng minh rằng
a) Tam giác ABC vuông tại C
b) CI⊥SB,DI⊥SC
c)CB⊥(SAC)
và các mặt bên hình chóp là các tam giác vuông
Cho hình chóp S.ABCD, đáy ABC là tam giác vuông cân tại B, AC=a căn 2, cạnh bên SA vuông góc với mặt phẳng đáy và SA= a căn 3.
Gọi M là trung điểm của SC. Tính góc của mặt phẳng (ABM) và mặt phẳng (ABC).
C
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB= 3a, BC = 4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và đáy bằng 60 o . Gọi M là trung điểm của AC, tính khoảng cách d giữa hai đường thẳng AB và SM.
A. d = a 3
B. d = 5 a 3
C. d = 5 a 2
D. d = 10 a 3 79