Đáp án D
Theo lý thuyết, một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tùy ý cho trước. Do đó hình biểu diễn của tam giác đều là một tam giác bất kì.
Đáp án D
Cho tam giác đều ABC như hình vẽ. tam giác OFB biến thành tam giác ODC qua phép biến hình nào sau đây?
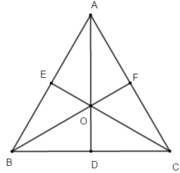
A. phép đối xứng tâm I
B. liên tiếp phép đối xứng trục AD và phép đối xứng trục CF
C. liên tiếp phép đối xứng tâm O và phép đối xứng trục OC
D. phép quay tâm A góc quay 60 o
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a Hình chiếu vuông góc của S lên (ABC )trùng với trung điểm H của cạnh BC biết tam giác SBC là tam giác đều tính số đo của góc giữa SA và (ABC)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 300
B. 450
C. 600
D. 900
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
A. 30 °
B. 75 °
C. 60 °
D. 45 °
Trong mặt phẳng (α) cho một tam giác ABC bất kì. Chứng minh rằng có thể xem tam giác ABC là hình chiếu song song của một tam giác đều nào đó.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm S lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác là SBC tam giác đều. Tính số đo của góc giữa đường thẳng SA và mặt phẳng (ABC)
A . 90 0
B . 60 0
C . 30 0
D . 45 0
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a. Biết SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy (ABC). Tính tang của góc tạo bởi đường thẳng SC và mặt đáy (ABC).
Cho đa giác đều có 15 đỉnh. Gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M, tính xác suất để tam giác được chọn là một tam giác cân nhưng không phải là tam giác đều.
A. 73 91
B. 18 91
C. 8 91
D. 18 19
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A . a 3 3 12
B . a 3 3 24
C . a 3 3 3
D . a 3 3 4
