Ta có:
\(\dfrac{2008}{2009}>\dfrac{2008}{2009+2010+2011}\)
\(\dfrac{2009}{2010}>\dfrac{2009}{2009+2010+2011}\)
\(\dfrac{2010}{2011}>\dfrac{2010}{2009+2010+2011}\)
Do đó: \(\dfrac{2008}{2009}+\dfrac{2009}{2010}+\dfrac{2010}{2011}>\dfrac{2008+2009+2010}{2009+2010+2011}\)
\(\Rightarrow A>B\)
`#PhuongYaa`
Ta có `B=2008+2009+2010/2009+2010+2011`
`=2008/2009+2010+2011 + 2009/2009+2010+2011 + 2010/2009+2010+2011`
`=>2008/2009+2010+2011 < 2008/2009`
`=>2009/2009+2010+2011 < 2009/2010` \(\left\{{}\begin{matrix}\dfrac{2008}{2009+2010+2011}+\dfrac{2009}{2009+2010+2011}+\dfrac{2010}{2009+2010+2011}\\\Rightarrow B< A\end{matrix}\right.\)
`=>2010/2009+2010+2011 <2010/2011`

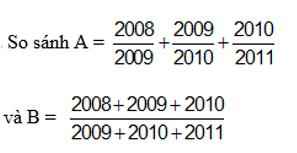














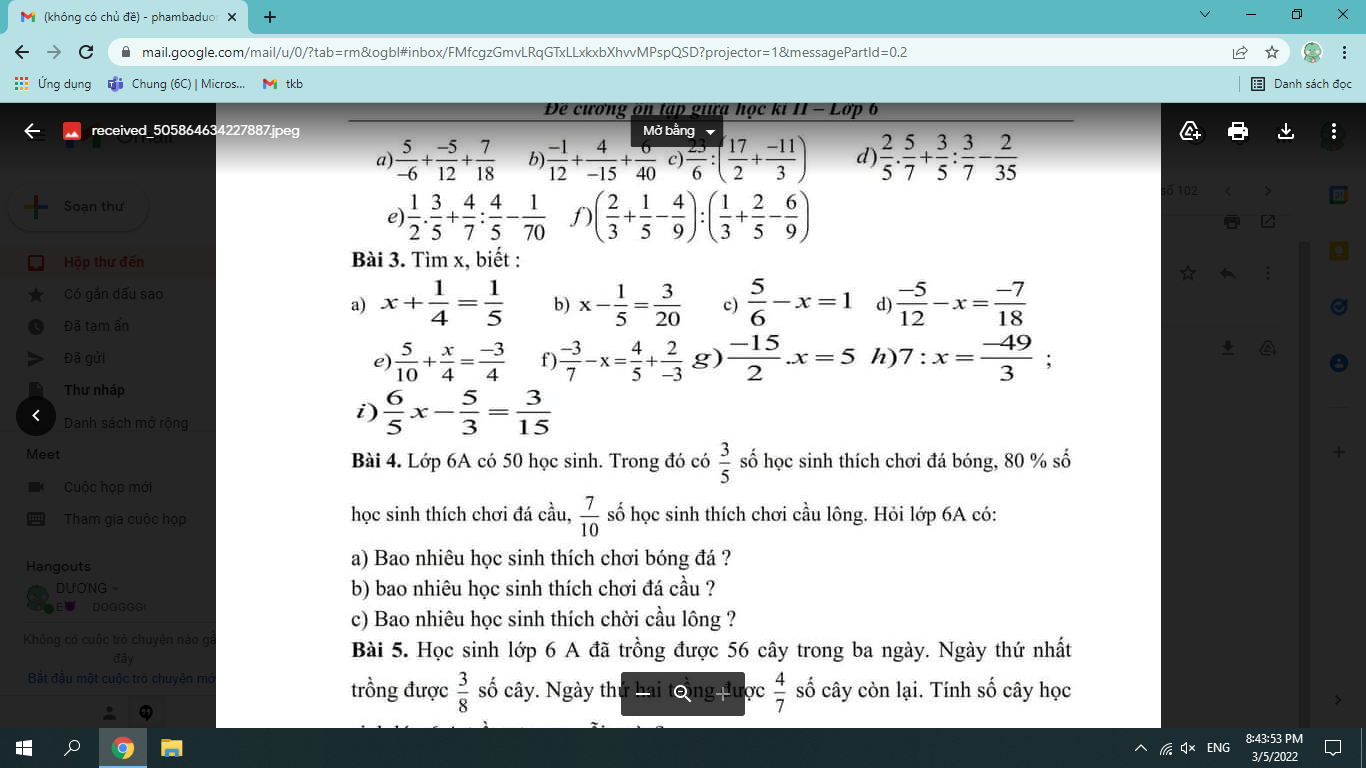 help bài 3 câu a ,b, và c help
help bài 3 câu a ,b, và c help




