Bài 1.1 TXĐ: $D=\mathbb{R}$
Bài 1.2:
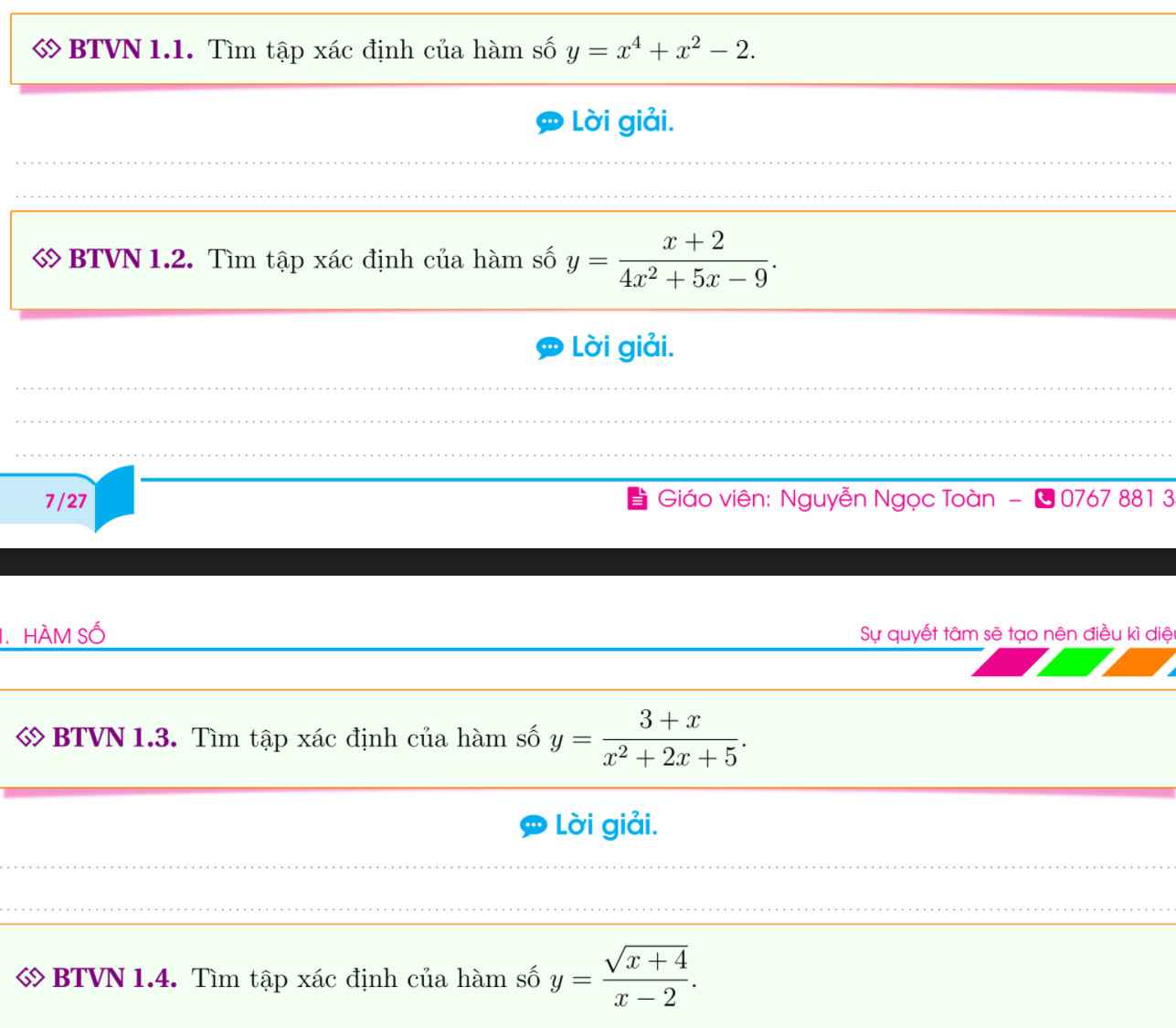
ĐKXĐ: $4x^2+5x-9\neq 0$
$\Leftrightarrow (x-1)(4x+9)\neq 0$
$\Leftrightarrow x\neq 1$ và $x\neq \frac{-9}{4}$
Vậy TXĐ: $D=\mathbb{R}\setminus \left\{1; \frac{-9}{4}\right\}$
Bài 1.3
ĐKXĐ: $x^2+2x+5\neq 0$
$\Leftrightarrow (x+1)^2+4\neq 0$
$\Leftrightarrow (x+1)^2\neq -4\Leftrightarrow x\in\mathbb{R}$
Vậy TXĐ: $D=\mathbb{R}$
Bài 1.4
ĐKXĐ: \(\left\{\begin{matrix} x+4\geq 0\\ x-2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -4\\ x\neq 2\end{matrix}\right.\)
Vậy TXĐ: $D=[-4;+\infty)\setminus \left\{2\right\}$
Bài 1.5
ĐKXĐ: $(2x-1)(x+3)\neq 0$
\(\Leftrightarrow \left\{\begin{matrix} 2x-1\neq 0\\ x+3\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq \frac{1}{2}\\ x\neq -3\end{matrix}\right.\)
Vậy TXĐ: $D=\mathbb{R}\setminus \left\{-3; \frac{1}{2}\right\}$
Bài 1.6:
ĐKXĐ: \(\left\{\begin{matrix} x-2\geq 0\\ x-3\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 2\\ x\neq 3\end{matrix}\right.\)
Vậy TXĐ: $D=[2;+\infty)\setminus \left\{3\right\}$
Bài 1.7:
ĐKXĐ: \(\left\{\begin{matrix} x-1\neq 0\\ x+2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 1\\ x\neq -2\end{matrix}\right.\)
TXĐ: $D=\mathbb{R}\setminus \left\{-2;1\right\}$
Bài 1.8:
ĐKXĐ: \(\left\{\begin{matrix} 4x+2\neq 0\\ -x+1>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{-1}{2}\\ x\leq 1\end{matrix}\right.\Leftrightarrow \frac{-1}{2}\leq x\leq 1\)
Vậy TXĐ: $D=[\frac{-1}{2}; 1]$
Bài 1.9:
ĐKXĐ: $|x-1|+|x-2|\neq 0$
Điều này luôn đúng với mọi $x\in\mathbb{R}$ do $|x-1|+|x-2|=|x-1|+|2-x|\geq |x-1+2-x|=1$ với mọi $x\in\mathbb{R}$
Vậy TXĐ: $D=\mathbb{R}$