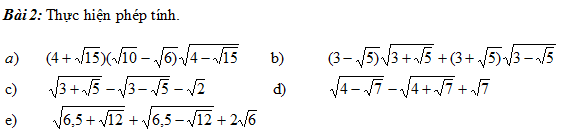\(a,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\\ b,=\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)\\ =\sqrt{4}\left(\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{1}{2}}+\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}\right)\\ =2\cdot2\sqrt{\dfrac{5}{2}}=4\sqrt{\dfrac{5}{2}}=2\sqrt{10}\\ c,=\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}-\sqrt{2}=2\sqrt{\dfrac{1}{2}}-\sqrt{2}=\sqrt{2}-\sqrt{2}=0\)
\(d,=\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{1}{2}}+\sqrt{7}\\ =-2\sqrt{\dfrac{1}{2}}+\sqrt{7}=\sqrt{7}-\sqrt{2}\)
\(e,=\sqrt{6}+\sqrt{\dfrac{1}{2}}+\sqrt{6}-\sqrt{\dfrac{1}{2}}+2\sqrt{6}=4\sqrt{6}\)