Tập xác định: D = R \{1}.
- Đạo hàm: 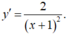
- Đồ thị hàm số cắt trục tung tại điểm A(0; -1)
⇒ y'(0) = 2.
Chọn B.
Tập xác định: D = R \{1}.
- Đạo hàm: 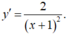
- Đồ thị hàm số cắt trục tung tại điểm A(0; -1)
⇒ y'(0) = 2.
Chọn B.
Hệ số góc của tiếp tuyến của đồ thị hàm số y = x - 1 x + 1 tại giao điểm với trục tung bằng
A. -2
B. 2
C. 1
D. -1
Hệ số góc của tiếp tuyến của đồ thị hàm số y = 2 - 3 x x - 1 tại giao điểm của đồ thị hàm số với trục hoành bằng
A. 9
B. 1 9
C. -9
D. - 1 9
Cho hàm số y = a x + b x - 1 có đồ thị cắt trục tung tại A(0; -1), tiếp tuyến tại A có hệ số góc k = -3. Các giá trị của a, b là
A. a = 1; b = 1
B. a = 2; b = 1
C. a = 1; b = 2
D. a = 2; b = 2
Cho hàm số y = a x + b x - 1 có đồ thị cắt trục tung tại A(0; -1), tiếp tuyến tại A có hệ số góc k = -3. Các giá trị của a, b là
A. a = 1; b = 1
B. a = 2; b = 1
C. a = 1; b = 2
D. a = 2; b = 2
Cho hàm số y = x + 2 2 x + 3 1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.
A: x + y = 0
B: x + y + 2 = 0
C: x + y – 2 = 0
D: Cả A và C đúng
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
cho hàm số y=x^3+3x^2+1 có đồ thị (C)/.Gọi d là tiếp tuyến của C tại điểm A(1,5) và B la giao điểm thứ hai của d với C khi đó diện tích tam giác oab bằng
Tiếp tuyến với đồ thị hàm số f ( x ) = ( x + 1 ) / ( 2 x - 3 ) tại điểm có hoành độ xo= 1 có hệ số góc bằng:
A. 13
B. -1
C. -5
D. -13
Tiếp tuyến của đồ thị hàm số y = f ( x ) = x 5 tại điểm mà tiếp điểm có tung độ bằng -1 có phương trình là:
A. y= 5x
B. y= -5x-6
C. y= 5x+6
D. y= 5x+4