Đáp án là B
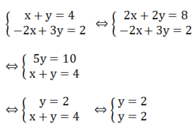
Vậy hệ phương trình có nghiệm (x; y)= (2; 2)
Đáp án là B
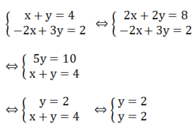
Vậy hệ phương trình có nghiệm (x; y)= (2; 2)
Biết hệ phương trình \(\left\{{}\begin{matrix}x+3y=1+m\\2x-y=7\end{matrix}\right.\) có nghiệm duy nhất (x0;y0) thỏa mãn x0+2y0.Khẳng định nào dưới đây là đúng?
A.-2≤m<0 B.0≤m<2 C.2≤m<4 D.4≤m<6
bài 1: giải các phương trình sau :
a) x^3-5x=0 b) căn bậc 2 của x-1=3
bài 2 :
cho hệ phương trình : {2x+my;3x-y=0 (I)
a) giải hệ phương trình khi m=0
b) tìm giá trị của m để hệ (I) có nghiệm (x;y) thỏa mãn hệ thức :
x-y+m+1/m-2=-4
bài 3:giải các phương trình sau
a)5x-2/3=5x-3/2 b) 10x+3/12=1+6x+8/9 c) 2(x+3/5)=5-(13/5+x) d) 7/8x-5(x-9)=20x+1,5/6
Bài 1 Cho hệ phương trình mx+4y=10-m và x+y=4
a, giải hệ phương trình khi m= căn 2
b, giải và biện luận hệ phương trình đã cho theo tham số m
c, trong trường hợp hệ có nghiệm duy nhất (x;y) tìm các giá trị của m để:
i, y-5x=-4. ii, x<1 và y>0
Bài 2: Cho hệ phương trình 2x+3y=m và 2x-3y=6 (m là tham số không âm)
a, giải hệ phương trình với m=3
b, tìm các giá trị của m để nghiệm (x;y) của hệ phương trình thoả mãn điều kiện x>0, y>0
Cho hệ phương trình \(\hept{\begin{cases}\left(m+1\right)x+2y=4-2m\\\left(2-m\right)x+my=1\end{cases}}\)
a) Để hệ phương trình là cặp số x>0, y<0
b) x2+y2 >=5
c) Có nghiệm là cặp số nguyên
bài 1: giải phương trình
x^4+x^2-12=0
bài 2 : cho hệ phương trình {mx-2y=4,x+my=5
a) giải hệ phương trình với m=3
b) tìm m để hệ phương trình có nghiệm duy nhất thỏa mãn x+y=5
bài 3 :cho y=x^2 (P) ; y=2mx+5 (d)
a) với m=2 tìm tọa độ giao điểm của (P) và (d)
giúp mình với mình đang cần gấp :>>
Cho hệ phương trình gồm 2 phương trình sau : (m-3)x+2y=6 và 3mx-y=-4 với m là tham số
a) Giải hệ phương trình với m=2
b) Tìm m để hệ phương trinhf có nghiệm duy nhất (x:y) thỏa mãn 2x+y>0
Giải phương trình nghiệm nguyên
a)
\(x^3-y^3-2y^2-3y-1=0\)
b)\(x^4-y^4+z^4+2x^2z^2+3x^2+4z^2+1=0\)
c) \(x^4+x^2-y^2+y+10=0\)
d) \(y^3=x^3+2x+1\)
1. Số nghiệm của hệ phương trình \(\hept{\begin{cases}x^3+2xy^2+12=0\\x^28y^2=12\end{cases}}\)
2. Giá trị nghuyên nhỏ nhất của m để phương trình \(x^3+mx=0\)có 3 nghiệm riêng biệt.
3. Tìm m để phương trình \(x^4-2x^2+3-1=0\)có 4 nghiệm mà điểm biễu diễn của chúng trên trục hoành cách đều nhau.
4. Cho hệ phương trình \(\hept{\begin{cases}mx+y=2m\\x+my=m+1\end{cases}}\)
Tìm giá trị nguyên âm của m để hệ phương trình trên có nghiệm (x;y) nguyên
14. Tìm m để phương trình m * x ^ 2 - 2(m - 2) * x + m - 3 = 0 có nghiệm duy nhất. A. m = 4 hoặc m = 0 B. m = 4 . C. m = 0 . D. 0 = m
Bài 1 : tìm các giá trị của m để phương trình có nghiệm kép : A. 3x² - 2mx + 1 = 0 B. 4mx² - 6x - m-3 = 0 C. (m+2) x² - 2 (m-1) x + 4 = 0 D. (m-6) x² + 3mx - 2 = 0