Định lí Cô sin : Tam giác ABC có AB = c, BC = a, AC = c thì ta có :
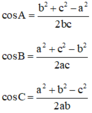
Định lí Cô sin : Tam giác ABC có AB = c, BC = a, AC = c thì ta có :
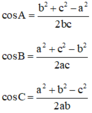
Tìm tính chất của tam giác ABC thỏa:
sinA+sinB+sinC=1-cosA+cosB+cosC
Cho tam giác ABC có góc A tù. Cho các biểu thức sau:
(1) M = sin A + sin B + sin C
(2) N = cosA. cosB. cosC
(3) P = cos A 2 . sin B 2 . c o t C 2
(4) Q = cotA.tan B.tan C
Số các biểu thức mang giá trị dương là:
A. 1
B. 2
C. 3
D. 4
Cho tam giác ABC. Từ các mệnh đề
P: “Tam giác ABC có hai góc bằng 60o ”
Q: “ABC là một tam giác đều”
Hãy phát biểu định lí P ⇒ Q. Nêu giả thiết, kết luận và phát biểu lại định lí này dưới dạng điều kiện cần, điều kiện đủ.
Trong hệ trục 0xy, cho A(1;1); B(2;4); C(10;-2)
a)Chứng minh tam giác ABC vuông
b)Tính \(\overrightarrow{BA}\).\(\overrightarrow{BC}\); cosB; cosC
Tam giác ABC vuông tại A có góc nhọn (ABC) ̂ = α. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9.
Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.
Cho tam giác ABC. Hãy chọn hệ thức đúng trong các hệ thức sau.
A. cos2A + cos2B + cos2C = 1 + cosA.cosB.cosC
B. cos2A + cos2B + cos2C = 1 - cosA.cosB.cosC
C. cos2A + cos2B + cos2C = 1 + 2cosA.cosB.cosC
D. cos2A + cos2B + cos2C = 1 + 3cosA.cosB.cosC
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?