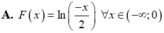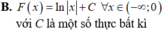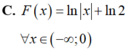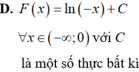Các câu hỏi tương tự
Xét các khẳng định sau: (1) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 1 điểm chung. (2) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 và f(0).f(1)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 2 điểm chung. Phát biểu nào sau đây đúng? A. Khẳng định đúng và khẳng định sai. B. Khẳng định sai và khẳng định đúng. C. Khẳng định sai và khẳng định sai. D. Khẳng định đúng và khẳng định đúng.
Đọc tiếp
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định 
đúng và khẳng định 
sai.
B. Khẳng định 
sai và khẳng định 
đúng.
C. Khẳng định 
sai và khẳng định 
sai.
D. Khẳng định 
đúng và khẳng định 
đúng.
Xét các khẳng định sau i) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn tại
α
∈
-
1
;
1
thỏa mãn
f
(
x
)
≥
f
(
α
)
∀
x
∈
-
1
;
1
. ii) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Biết luôn có hai số a, b để
F
(
x
)
a
x
+
b
x
+
4
(
4
a
-
b
≠
0
)
là nguyên hàm của hàm số f(x) và thỏa mãn
2
f
2
(
x
)
...
Đọc tiếp
Biết luôn có hai số a, b để F ( x ) = a x + b x + 4 ( 4 a - b ≠ 0 ) là nguyên hàm của hàm số f(x) và thỏa mãn 2 f 2 ( x ) = ( F ( x ) - 1 ) f ' ( x ) . Khẳng định nào dưới đây đúng và đầy đủ nhất?
Gọi F(x) là một nguyên hàm của hàm số f(x) xcosx thỏa mãn F(0) 1. Khi đó phát biểu nào sau đây đúng? A. F(x) là hàm số chẵn. B. F(x) là hàm số lẻ. C. Hàm số F(x) tuần hoàn với chu kì là . D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.
Đọc tiếp
Gọi F(x) là một nguyên hàm của hàm số f(x) = xcosx thỏa mãn F(0) = 1. Khi đó phát biểu nào sau đây đúng?
A. F(x) là hàm số chẵn.
B. F(x) là hàm số lẻ.
C. Hàm số F(x) tuần hoàn với chu kì là 
.
D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.
Cho hàm số yf(x) liên tục trên R thỏa mãn
∫
f
(
x
)
d
x
e
-
2018
x
+
C
. Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R thỏa mãn ∫ f ( x ) d x = e - 2018 x + C . Khẳng định nào sau đây là đúng?
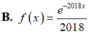
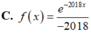
Cho K là một khoảng và hàm số yf(x) có đạo hàm trên K. Giả sử f (x)0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng? A. Nếu thì hàm số là hàm hằng trên K. B. Nếu thì hàm số nghịch biến trên K. C. Nếu thì hàm số đồng biến trên K. D. Nếu thì hàm số nghịch biến trên K.
Đọc tiếp
Cho K là một khoảng và hàm số y=f(x) có đạo hàm trên K. Giả sử f '(x)=0 chỉ tại một số hữu hạn điểm trên K. Khẳng định nào sau đây là đúng?
A. Nếu 
thì hàm số là hàm hằng trên K.
B. Nếu 
thì hàm số nghịch biến trên K.
C. Nếu 
thì hàm số đồng biến trên K.
D. Nếu 
thì hàm số nghịch biến trên K.
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
x
-
1
thỏa mãn F(5) 2 và F(0) 1. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5) = 2 và F(0) = 1. Mệnh đề nào dưới đây đúng?
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn
[
f
(
x
)
]
4
.
[
f
(
x
)
]
2
(
x
2
+
1
)
1...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn [ f ( x ) ] 4 . [ f ' ( x ) ] 2 ( x 2 + 1 ) = 1 + f 3 ( x ) và f(x)>0 biết f(0) = 2 Hãy chọn khẳng định đúng trong các khẳng định sau:
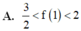
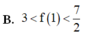
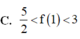
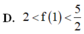
Cho hàm số y f(x) có
lim
x
→
+
∞
f
(
x
)
0
và
lim
x
→
0
+
f
(
x
)
+
∞
. Khẳng địn...
Đọc tiếp
Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 0 và lim x → 0 + f ( x ) = + ∞ . Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng
B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho
C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y = 0
D. Hàm số đã cho có tập xác định là D = (0; +∞)