Đáp án A.
Hàm số y = 4 x 2 - 1 - 4 xác định ⇔ 4 x 2 - 1 ≠ 0 ⇔ x ≠ ± 1 2
Vậy tập xác định của hàm số là D = ℝ \ - 1 2 ; 1 2 .
Đáp án A.
Hàm số y = 4 x 2 - 1 - 4 xác định ⇔ 4 x 2 - 1 ≠ 0 ⇔ x ≠ ± 1 2
Vậy tập xác định của hàm số là D = ℝ \ - 1 2 ; 1 2 .
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019;2019) để hàm số sau có tập xác định là D = ℝ
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
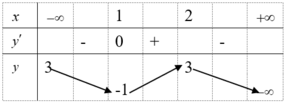
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
![]()
![]()
![]()
![]()
Cho hàm số y = x − 2 x − 1 . Xét các mệnh đề sau:
1. Hàm số đã cho đồng biến trên − ∞ ; 1 ∪ 1 ; + ∞ .
2. Hàm số đã cho đồng biến trên ℝ \ 1 .
3. Hàm số đã cho đồng biến trên từng khoảng xác định.
4. Hàm số đã cho đồng biến trên các khoảng − ∞ ; − 1 và − 1 ; + ∞ .
Số mệnh đề đúng là
A. 3
B. 2
C. 1
D. 4
Cho hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 . Tập giá trị của m để y ' ≥ 0 ∀ x ∈ ℝ là
A. [3;+ ∞ )
B. ∅
C. [ 4 2 ;+ ∞ )
D. [1;+ ∞ )
Cho hàm số y = f(x) xác định và liên tục trên ℝ \ { 0 } thỏa mãn: x 2 f 2 ( x ) + ( 2 x - 1 ) f ( x ) = x f ' ( x ) - 1 đồng thời f ( 1 ) = - 2 Tính ∫ 1 2 f ( x ) d x
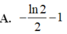
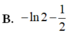
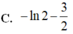
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ ℝ . Số điểm cực trị của hàm số f(x) là
A. 0
B. 3
C. 2
D. 1
Cho hàm số y=f(x) xác định trên ℝ \ - 1 và liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
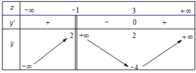
Số nghiệm của phương trình f ( 2 x - 3 ) + 4 = 0 là:
A. 4
B. 3
C. 2
D. 1
Có bao nhiêu giá trị nguyên của tham số m trên [-2018;2018] để hàm số y = ln ( x 2 - 2 x - m + 1 ) có tập xác định là ℝ ?
A. 2019
B. 2017
C. 2018
D. 1009
Cho hàm số f(x) có đạo hàm trên ℝ và f''(x) > 0, ∀ x ∈ ℝ . Biết f(1) = 2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1)= 2
C. f(2) = 1
D. f(2018) > f(2019)
Tìm tất cả các giá trị thực của tham số m để hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ .
A. m > -4
B. m < 0
C. m < -4
D. m < -3