Chọn: A
Xét đáp án A ta có:
![]()
và y ' = - 4 x + 2 2 < 0 ∀ x ∈ D
Vậy hàm số y = - x + 2 x + 2 nghịch biến trên mỗi khoảng xác định của nó.
Chọn: A
Xét đáp án A ta có:
![]()
và y ' = - 4 x + 2 2 < 0 ∀ x ∈ D
Vậy hàm số y = - x + 2 x + 2 nghịch biến trên mỗi khoảng xác định của nó.
Xác định giá trị của tham số m để hàm số y = x 2 + m + 1 x - 1 2 - x
nghịch biến trên mỗi khoảng xác định của nó
A. m = −1; B. m > 1;
C. m ∈ (−1;1); D. m ≤ −5/2.
Cho hàm số: y = x - 2 x + 3
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên từng khoảng xác định;
B. Hàm số đồng biến trên khoảng (- ∞ ;+ ∞ );
C. Hàm số nghịch biến trên từng khoảng xác định;
D. Hàm số nghịch biến trên khoảng (- ∞ ;+ ∞ ).
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên mỗi khoảng xác định của nó.
![]()
![]()
![]()
![]()
Trong bốn hàm số y = x + 1 x + 2 , y = 5 x + 6 x 2 x , y = π 6 x , y = log 3 x có bao nhiêu hàm số đồng biến trên mỗi khoảng xác định của nó?
A. 1
B. 3
C. 2
D. 4
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ -1
B. m < 1.
C. m < -3.
D. m ≤ -3
Cho hàm số y= f(x) có đạo hàm trên R thoả f( 2) = f( -2) =0 và đồ thị của hàm số y= f’ (x) có dạng như hình bên. Hàm số y= (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
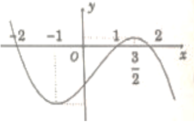
A. - 1 ; 3 2
B. (-1; 1)
C. (-2; -1)
D. (1; 2)
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0
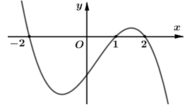
Hàm số g( x) = [ f( 3-x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1)
B. (1; 2)
C. (2; 5)
D. ( 5 ; + ∞ )
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Khi đó hàm số y = f x 2 nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Cau 1: Hàm số y= \(\frac{x}{\sqrt{x^2-x}}\) nghịch biến trên khoảng nào?
Cau 2: Hàm số y=\(x+\sqrt{2x^2+1}\)nghịch biến trên khoảng nào?
Hàm số y = ( x 2 - x ) 2 nghịch biến trên khoảng nào dưới đây?

![]()
![]()
![]()