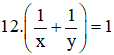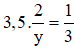Hai đội công nhân cùng làm một công việc và dự định làm xong trong 12 ngày . Họ cùng làm với nhau được 8 ngày thì đội 1 được điều đi làm việc khác và đội 2 tiếp tục làm , do cải tiến kĩ thuật năng xuất tăng gấp đôi nên đội 2 đã hoàn thành phần việc trong 3 ngày rưỡi . Hỏi nếu mỗi đội làm 1 mình thì dau bao lâu sẽ làm xong công việc nói trên với năng xuất bình thường .
Trả lời:
Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)
Điều kiện : x, y > 12, x,y ∈ N.
Một ngày đội I làm được :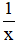 
(công việc).
Một ngày đội II làm được :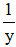 
(công việc).
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: 
+ Hai đội cùng làm trong 8 ngày được: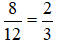 
công việc.
⇒ còn lại đội II phải hoàn thành một mình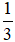 
công việc.
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được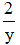 
công việc.
Đội II hoàn thành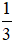 
công việc còn lại trong 3,5 ngày nên ta có phương trình: 
Ta có hệ phương trình:
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.
Gọi x , y lần lượt là số thời gian đội 1 và đội 2 hoàn thành xong công việc
Trong 1 ngày , đội 1 làm xong \(\frac{1}{x}\) công việc .
Trong 1 ngày , đội 2 làm được \(\frac{1}{y}\)công việc .
Trong 1 ngày , cả 2 đội làm được \(\frac{1}{12}\) công việc .
Theo bài cho ta có : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\) ( 1 )
Khi cả 2 đội làm chung 8 ngày , cả hai đội làm được \(\frac{8}{12}=\frac{2}{3}\)công việc .
Vậy số công việc để 2 đội làm nốt là : \(1-\frac{2}{3}=\frac{1}{3}\) công việc
Mà đội 2 làm với năng suất tăng gấp đôi nên : \(2.\frac{1}{y}=\frac{2}{y}\)
Ta lại có : \(3,5.\frac{2}{y}=\frac{1}{3}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra : x = 28 , y = 21
Vậy đội 1 làm trong 28 ngày , đội 2 làm trong 21 ngày .
Học tốt
