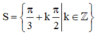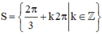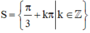`\sqrt{3} sin 2x-cos 2x=2`
`<=>\sqrt{3}/2 sin2x-1/2cos 2x=1`
`<=>sin` `\pi/3 .sin 2x-cos` `\pi/3 .cos 2x=1`
`<=>cos(\pi/3 +2x)=-1`
`<=>\pi/3 + 2x=\pi+k2\pi` , `k in ZZ`
`<=>x=\pi/3+k\pi` , `k in ZZ`
\(Ta có:\) \(\sqrt{a^2+b^2}=\sqrt{\sqrt{3}^2+1^2}=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}\sin2x-\dfrac{1}{2}\cos2x=1\)
\(\Leftrightarrow\sin2x\cdot\cos\dfrac{\pi}{6}-\cos2x\cdot\sin\dfrac{\pi}{6}=1\)
\(\Leftrightarrow\sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow2x=\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\) \(\left(k\in Z\right)\)