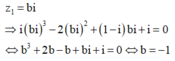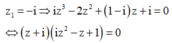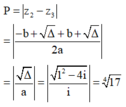Các câu hỏi tương tự
Tìm số phức z biết |iz + 1 | = 2 và ( 1 + i) z + 1 – 2i là số thuần ảo.
A. z = 1
B. z = 1 + 2i
C. z = - 1 và z = 1+ 2i
D. Đáp án khác
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| |
z
¯
+ 2 + 4i| và
z
-
i
z
¯
+
i
là số thuần ảo.
Đọc tiếp
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| z ¯ + 2 + 4i| và z - i z ¯ + i là số thuần ảo.
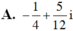
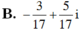

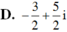
Có bao nhiêu số phức z thỏa mãn các điều kiện
z
-
2
+
i
2
v
à
(
z
+
i
)
2
là số thuần ảo?
Đọc tiếp
Có bao nhiêu số phức z thỏa mãn các điều kiện z - 2 + i = 2 v à ( z + i ) 2 là số thuần ảo?
![]()
![]()
![]()
![]()
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với ...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Trong tập hợp các số phức, gọi
z
1
;
z
2
là nghiệm của phương trình
z
2
-
z
+
2017
4
0
, với
z
2
có thành phần ảo dương. Cho số phức
z
thoả mãn
z
-
z...
Đọc tiếp
Trong tập hợp các số phức, gọi z 1 ; z 2 là nghiệm của phương trình z 2 - z + 2017 4 = 0 , với z 2 có thành phần ảo dương. Cho số phức z thoả mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Trong tập các số phức, gọi
z
1
,
z
2
là hai nghiệm của phương trình
z
2
-
z
+
2017
4
0
với
z
2
có thành phần ảo dương. Cho số phức z thỏa mãn
z
-
z...
Đọc tiếp
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
![]()
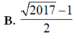
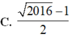
![]()
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z-1+1| |z+i-2| là đường thẳng có phương trình
Đọc tiếp
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z-1+1| = |z+i-2| là đường thẳng có phương trình
![]()
![]()
![]()
![]()
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| |
z
¯
+ 3 + 4i| và
z
-
2
i
z
¯
+
i
là một số thuần ảo.
Đọc tiếp
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | z ¯ + 3 + 4i| và z - 2 i z ¯ + i là một số thuần ảo.
![]()
![]()
![]()