Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.ABCD có AA a, AB 2a, AD 3a. Gọi V là phần thể tích thuộc hình hộp nằm ở khoảng giữa hai mặt phẳng (ABD) và (BCD). Tính V. A. V 4
a
3
B. V 3
a
3
C. V 2
a
3
D. V
a
3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = 2a, AD = 3a. Gọi V là phần thể tích thuộc hình hộp nằm ở khoảng giữa hai mặt phẳng (A'BD) và (B'CD'). Tính V.
A. V = 4 a 3
B. V = 3 a 3
C. V = 2 a 3
D. V = a 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
,
B
,
C
,
D
,
có tâm I. Gọi
V
,
V
1
lần lượt là thể tích của khối hộp
A
B
C
D
.
A
,
B
,
C
,
D
,
và khối...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A , B , C , D , có tâm I. Gọi V , V 1 lần lượt là thể tích của khối hộp A B C D . A , B , C , D , và khối chóp I . A B C D Tính tỉ số k = V 1 V .
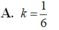
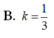
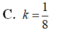
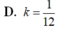
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a
3
, BD3a. Hình chiếu vuông góc của B trên mặt phẳng (ABCD) trùng với trung điểm A’C’. Gọi
α
là góc giữa 2 mặt phẳng (ABCD) và (CDDC). Thể tích của khối hộp ABCD.ABCD bằng
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , BD=3a. Hình chiếu vuông góc của B trên mặt phẳng (A'B'C'D') trùng với trung điểm A’C’. Gọi α là góc giữa 2 mặt phẳng (ABCD) và (CDD'C'). Thể tích của khối hộp ABCD.A'B'C'D' bằng
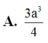
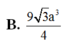
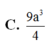
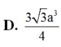
Cho hình hộp ABCD.ABCD. Gọi E, F tương ứng là trung điểm các cạnh A’A, C’C. Mặt phẳng (D’EF) chia hình hộp thành hai hình đa diện. Gọi (H) là hình đa diện chứa đỉnh A, (H’) là hình đa diện còn lại. Tính tỉ số k giữa thể tích hình (H) và thể tích hình (H’). A.
k
1
3
B.
k
2
3
C.
k
3
4...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm các cạnh A’A, C’C. Mặt phẳng (D’EF) chia hình hộp thành hai hình đa diện. Gọi (H) là hình đa diện chứa đỉnh A, (H’) là hình đa diện còn lại. Tính tỉ số k giữa thể tích hình (H) và thể tích hình (H’).
A. k = 1 3
B. k = 2 3
C. k = 3 4
D. k = 1
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC a/2, SC BC a
2
. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k V/V. A.
k
1
3
B.
k
2
4
C.
k...
Đọc tiếp
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

A. k = 1 3
B. k = 2 4
C. k = 4 9
D. k = 2 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có tâm I. Gọi V,
V
1
lần lượt là thể tích của khối hộp
A
B
C
D
.
A
B
C
D
và khối chóp I.ABCD. Tính tỉ số
k
V
1
V
A. ...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có tâm I. Gọi V, V 1 lần lượt là thể tích của khối hộp A B C D . A ' B ' C ' D ' và khối chóp I.ABCD. Tính tỉ số k = V 1 V
A. k = 1 6
B. k = 1 3
C. k = 1 8
D. k = 1 12
Cho hình hộp chữ nhật ABCD.ABCD có
A
B
B
C
a
;
A
A
a
3
. Gọi I là giao điểm của AD và A’D ; H là hình chiếu của I trên mặt phẳng
A
B
C
D
, K là hình chiếu của B lên mặt phẳng...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A B = B C = a ; A ' A = a 3 . Gọi I là giao điểm của AD' và A’D ; H là hình chiếu của I trên mặt phẳng A ' B ' C ' D ' , K là hình chiếu của B lên mặt phẳng C A ' B ' . Tính thể tích khối tứ diện IHBK ?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 16
D. a 3 3 8
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm O, cạnh bằng a, BDa
3
. Góc giữa CC’ và mặt đáy là
60
0
, trung điểm H của AO là hình chiếu vuông góc của A’ lên mặt phẳng ABCD. Tính thể tích của hình hộp
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm O, cạnh bằng a, B'D'=a 3 . Góc giữa CC’ và mặt đáy là 60 0 , trung điểm H của AO là hình chiếu vuông góc của A’ lên mặt phẳng ABCD. Tính thể tích của hình hộp
![]()
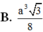
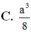
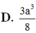
Cho hình hộp ABCD.A’B’C’D’ . Gọi E và F lần lượt là trung điểm của B’C’ và C’D’ . Mặt phẳng (AEF) chia hình hộp đó thành hai hình đa diện (H) và (H’), trong đó (H) là hình đa diện chứa đỉnh A’. Tính tỉ số giữa thể tích hình đa diện (H) và thể tích hình đa diện (H’).



