Các câu hỏi tương tự
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên. A. 1 B. 0 C. 2 D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số 
có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
A. 1
B. 0
C. 2
D. 4
Tìm tất cả các giá trị của tham số m sao cho đường thẳng y 2m-1 cắt đồ thị hàm số
y
x
3
-
3
x
+
1
tại 4 điểm phân biệt A.
0
≤
m
≤
1
B.
m
≥
1
C.
0
m
1
D. m 0
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho đường thẳng y= 2m-1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. 0 < m < 1
D. m < 0
Tìm m để đồ thị hàm số
y
x
3
+
3
x
2
+
m
x
+
2
m
cắt đường thẳng y -x + 2 tại 3 điểm. A.
m
5
4
B. m 1 C.
m
5
4
và
m
≠
-
1
D.
-
1
m
5...
Đọc tiếp
Tìm m để đồ thị hàm số y = x 3 + 3 x 2 + m x + 2 m cắt đường thẳng y = -x + 2 tại 3 điểm.
A. m > 5 4
B. m > 1
C. m < 5 4 và m ≠ - 1
D. - 1 < m < 5 4
Cho đồ thị hàm số
y
x
3
-
2
x
2
+
2
x
.
Gọi
x
1
,
x
2
là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y -x + 2016. Khi đó
x
1
+
x
2
bằng: A.
4
3...
Đọc tiếp
Cho đồ thị hàm số y = x 3 - 2 x 2 + 2 x . Gọi x 1 , x 2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016. Khi đó x 1 + x 2 bằng:
A. 4 3
B. - 4 3
C. 1 3
D. -1
Cho hàm số
y
x
4
2
-
2
m
2
x
2
+
2
. Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình ph...
Đọc tiếp
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
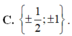
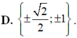
Hệ số góc của tiếp tuyến của đồ thị hàm số y = x - 1 x + 1 tại giao điểm của đồ thị hàm số với trục tung bằng
A. -2
B. 2
C. -1
D. 1
Cho hàm số f(x) liên tục trên [-1;3] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên [-1;3]. Tính M - m.
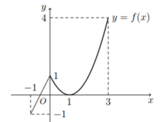
A. 3
B. 4
C. 5
D. 1
Tìm m để đồ thị hàm số y = x + m m x + 1 có đường tiệm cận ngang
A. m ≠ 0
B. m ≠ ±1
C. m ≠ 1
D. Cả A và B
Cho hàm số
y
f
(
x
)
có bảng biến thiên như hình bên. Tọa độ điểm cực đại của đồ thị hàm số
y
f
(
x
)
là A.
M
(
0
;
-
3
)
B.
N
(
-
1
;
-
4
)
C.
P
(
1
;
-
4
)...
Đọc tiếp
Cho hàm số y = f ( x ) có bảng biến thiên như hình bên. Tọa độ điểm cực đại của đồ thị hàm số y = f ( x ) là
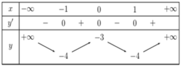
A. M ( 0 ; - 3 )
B. N ( - 1 ; - 4 )
C. P ( 1 ; - 4 )
D. Q ( - 3 ; 0 )