Chọn: A
![]()
hàm số đã cho trở thành
![]()
Ta có:
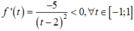
⇒ f t nghịch biến trên [-1; 1]
![]()
![]()
![]()
Chọn: A
![]()
hàm số đã cho trở thành
![]()
Ta có:
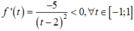
⇒ f t nghịch biến trên [-1; 1]
![]()
![]()
![]()
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = sin x + 1 3 - 2 sin x . Khi đó ta có
A. M + 2019m = 2.
B. M - 2019m = -2019.
C. 2M + 3m = 0.
D. M + m = 1.
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có
A. 9M + m = 0
B. 9M - m = 0
C. M + 9m = 0
D. M + m = 0
Cho hàm số f(x) liên tục trên (0;+ ∞ ) thỏa mãn 3x.f(x) - x 2 f ' ( x ) = 2 f 2 ( x ) , với f(x) ≠ 0, ∀ x ∈ (0;+ ∞ ) và f(1) = 1 3 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính M + m.
A. 9 10
B. 21 10
C. 7 3
D. 5 3
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 sin x + 2 sin x + 1 trên đoạn 0 ; π 2 . Khi đó giá trị của M 2 + m 2 là
A. 31 2
B. 11 2
C. 41 4
D. 61 4
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(1-2cos x) trên 0 ; 3 π 2 . Giá trị của M + m bằng
A. 2
B. 1
C. 1 2
D. 3 2
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 3 + 3 trên đoạn [0; 2]. Tính giá trị của biểu thức M + 2m.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hai số thực x , y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log ( 11 - 2 x - y ) = 2 x + 4 y - 1 Xét biểu thức P = 16 x 2 y - 2 x ( 3 y + 2 ) - y + 5 . Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4 m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
Cho hàm số y = x 4 - 4 x 3 + 4 x 2 + a . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
A. 4
B. 5
C. 6
D. 3
Cho hàm số f ( x ) = x 4 - 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] .Có bao nhiêu số nguyên a thuộc đoạn [-3; 3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5