Question

Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng: Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

Answer 1

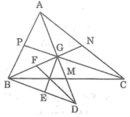
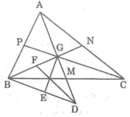
Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.

Ta có: AG = GD (gt)

AG = 2GM (tính chất đường trung tuyến)

Suy ra: GD = 2GM

Mà GD = GM + MD ⇒ GM = MD

Xét ΔBMD và ΔCMG, ta có:

BM = CM (gt)

∠(BMD) = ∠(CMG) (đối đỉnh)

MD = GM (chứng minh trên)

Suy ra: ΔBMD = ΔCMG (c.g.c)

⇒ BD = CG (hai cạnh tương ứng)

Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)

Suy ra: BD = 2/3 CP (1)

Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)

Và AG = 2/3 AM (tính chất đường trung tuyến)

Suy ra: GD = 2/3 AM (3)

Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.