Chọn đáp án D
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Chọn đáp án D
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Mỗi câu sau đây đúng hay sai
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Nêu cách tính số đo của góc tạo bởi tia tiếp tuyến và dây cung theo số đo của cung bị chắn.
Nêu cách tính số đo của góc tạo bởi tia tiếp tuyến và dây cung theo số đo của cung bị chắn.
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Hãy vẽ hình minh họa các tính chất trên.
Góc nội tiếp (nhỏ hơn hoặc bằng 90o) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung
a) Hãy vẽ góc BAx tạo bởi tia tiếp tuyến và dây cung trong ba trường hợp sau:
BAx ^ = 30 ° , BAx ^ = 90 ° , BAx ^ = 120 °
b) Trong mỗi trường hợp ở câu a), hãy cho biết số đo của cung bị chắn.
Cung BmC có số đo bằng 40° , góc ở nội tâm chắn cung BmC có số đo bằng a.20° b.70° c.30° d.40°
Hãy vẽ góc BAx tạo bởi tia tiếp tuyến và dây cung trong ba trường hợp sau:
a) B A x ^ = 30 o , B A x ^ = 90 o , B A x ^ = 120 o
b) Trong mỗi trường hợp ở câu a), hãy cho biết số đo của cung bị chắn.
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
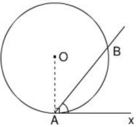
Hình 29
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
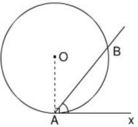
Hình 29