Chọn đáp án A
Cho đường tròn tâm (O) có Ax là tia tiếp tuyến tại điểm A và dây cung AB. Khi đó góc BAx là góc tạo bởi tia tiếp tuyến và dây cung
Chọn đáp án A
Cho đường tròn tâm (O) có Ax là tia tiếp tuyến tại điểm A và dây cung AB. Khi đó góc BAx là góc tạo bởi tia tiếp tuyến và dây cung
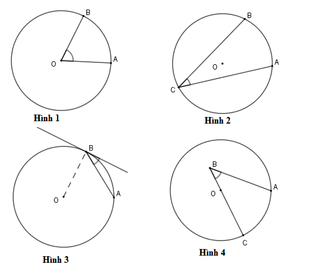
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung
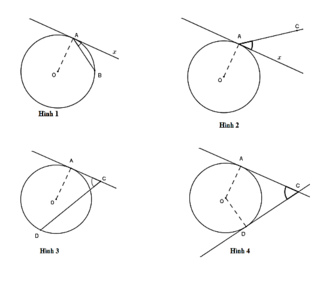
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
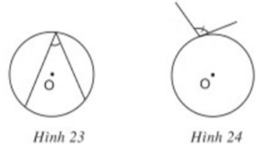
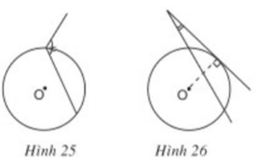
Hãy giải thích vì sao các góc ở hình 23, 24, 25, 26 không phải là góc tạo bởi tia tiếp tuyến và dây cung.
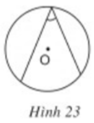
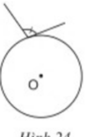
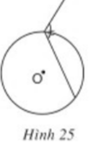
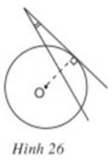
Hãy giải thích vì sao các góc ở hình 23, 24, 25, 26 không phải là góc tạo bởi tia tiếp tuyến và dây cung.
Trong hình 67, cung AmB có số đo là 60 ° . Hãy:
a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.
b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.
c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB
e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh cung AEB với cung ACB
Trong hình 67, cung AmB có số đo là 60o. Hãy:
Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.
1. AB là một cung của (O;R) với sđ cung AB nhỏ là 80 độ. khi đó , góc AOB có số đo là?
2. cho đường tròn (O;R) và dây AB=R. trên cung AB lớn lấy điểm M. số đo cung AMB là?
3. số đo góc tạo bởi tia tiếp tuyến và dây cung bằng?
4. hình tròn ngoại tiếp lục giác đều cạnh 5 cm có diện tích là?
Hình nào dưới đây biểu diễn góc nội tiếp?
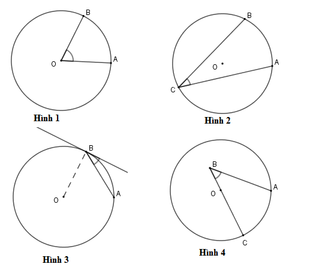
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hình nào dưới đây biểu diễn góc nội tiếp?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Từ điểm M nằm ngoài đường tròn, kẻ hai tiếp tuyến MN, MP.
c) Tính diện tích hình tạo bởi hai tiếp tuyến và đường tròn.
d) Tính diện tích hình viên phân tạo bởi dây AB và cung AB.