a) ĐKXĐ : \(x\ne\pm1\)
Khi đó \(\frac{3x-2}{x-1}-\frac{x+3}{x+1}=2\)
=> \(\frac{\left(3x-2\right)\left(x+1\right)-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{2\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\)
=> (3x - 2)(x + 1) - (x + 3)(x - 1) = 2(x - 1)(x + 1)
<=> 3x2 + x - 2 - (x2 + 2x - 3) = 2x2 - 2
<=> 2x2 - x + 1 = 2x2 - 2
<=> x = 3 (tm)
Vạy x = 3 là nghiệm phương trình
b) 4x2 - 1 = (x - 5)(1 - 2x)
<=> (2x - 1)(2x +1) = -(x - 5)(2x - 1)
<=> (2x - 1)(2x + 1) + (x - 5)(2x - 1) = 0
<=> (2x - 1)(2x + 1 + x - 5) = 0
<=> (2x - 1)(3x - 4) = 0
<=> \(\orbr{\begin{cases}2x-1=0\\3x-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{4}{3}\end{cases}}\)
Vậy \(x\in\left\{\frac{1}{2};\frac{4}{3}\right\}\)là nghiệm phương trình
c) \(\frac{x-3}{3}-\frac{2x-1}{2}>2\)
<=> \(\frac{2\left(x-3\right)-3\left(2x-1\right)}{6}>\frac{12}{6}\)
<=> 2(x - 3) - 3(2x - 1) > 12
<=> 2x - 6 - 6x + 3 > 12
<=> -4x > 15
=> x < -15/4
Vậy x < -15/4 là nghiệm bất phương trình







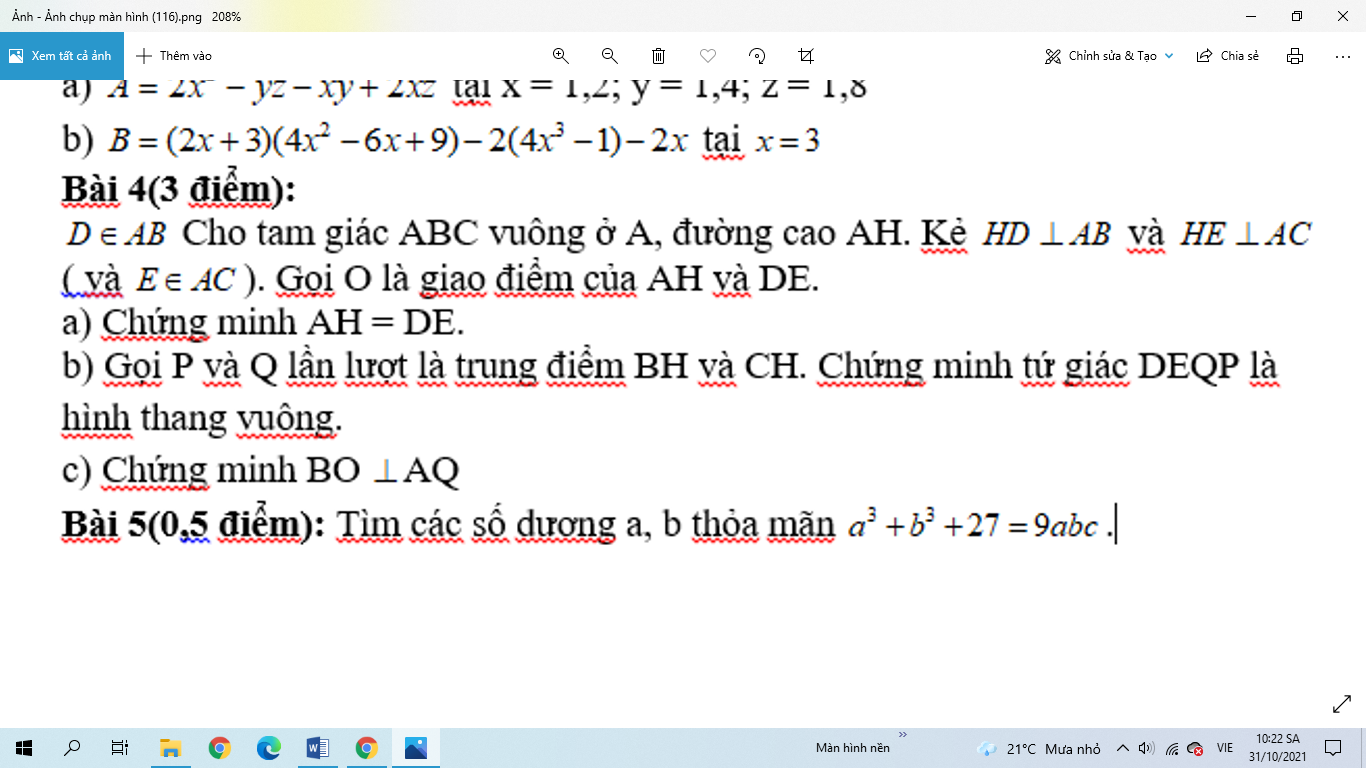


 Giups mình câu b ạ
Giups mình câu b ạ 







