a) \(\dfrac{x-1}{5}\)=\(\dfrac{3}{y+4}\)
⇒( x - 1)( y + 4) = 3.5 = (-3)(-5) = 5.3 = (-5)(-3) = 1.15 = (-1)(-15)
| x - 1 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| x
| 2 | 0 | 4 | -2 | 6 | -4 | 16 | -14 |
| y + 4 | 15 | -15 | 5 | -5 | 3 | -3 | 1 | -1 |
| y | 11 | -19 | 1 | -9 | -1 | -7 | -3 | -5 |
Vậy \(\left\{{}\begin{matrix}x=2\\y=11\end{matrix}\right.\); \(\left\{{}\begin{matrix}x=0\\y=-19\end{matrix}\right.\); \(\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\);.........\(\left\{{}\begin{matrix}x=-14\\y=-5\end{matrix}\right.\)
b) A= 1+\(3^2\)+\(2^2\).\(3^3\)+\(3^2\).\(3^2\)+\(3^2\).\(4^2\)+\(3^2\).\(5^2\)+\(3^2\).\(6^2\)+.....\(3^2\).\(12^2\)
=\(3^2\).(\(\dfrac{1}{3}^2\)+\(2^2\)+\(3^2\)+\(4^2\)+\(5^2\)+\(6^2\)+......+\(12^2\))
=9.(\(\dfrac{1}{9}\)+649)=5842
b) Vì \(2^2+3^2+...+12^2=649\)
\(=>3^2\left(2^2+3^2+...+12^2\right)=3^2\cdot649\)
\(=>6^2+9^2+...+36^2=5841\)
=> A = \(1+9+5841\) = 5851

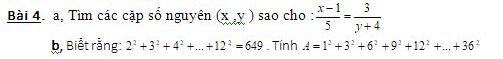 giúp vs ạ:33
giúp vs ạ:33








 giúp em với ạ nhanh em cần ạ :33
giúp em với ạ nhanh em cần ạ :33


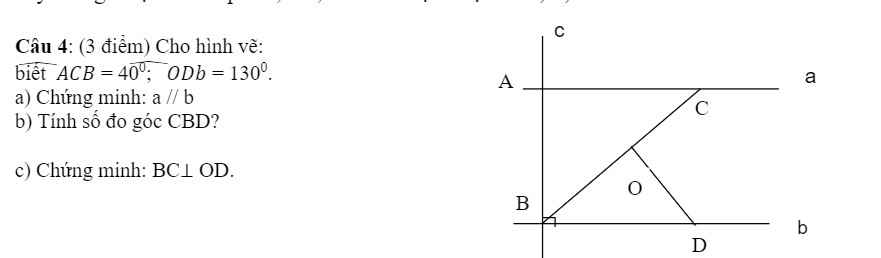 mk vs ạ
mk vs ạ

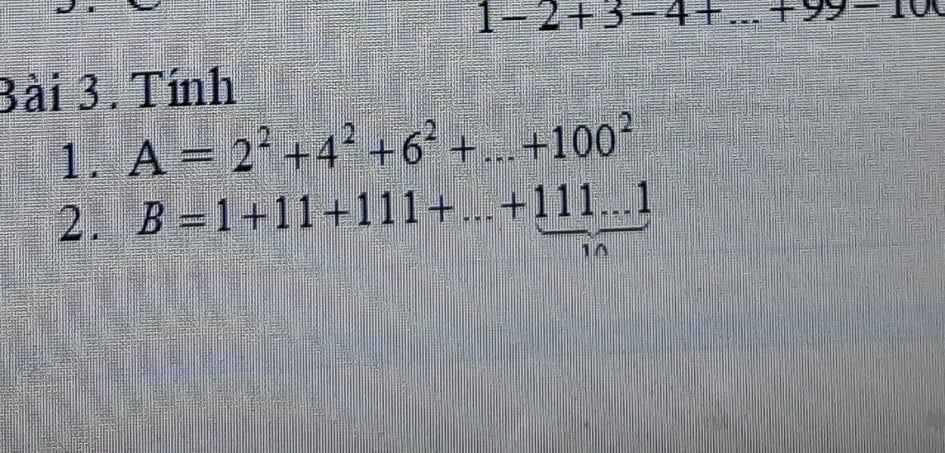 mng giúp em câu a với ạ <33 em cảm ơn
mng giúp em câu a với ạ <33 em cảm ơn