-Công thức tính \(1+2+...+n=\dfrac{\left(\dfrac{n-1}{1}+1\right)\left(n+1\right)}{2}=\dfrac{n\left(n+1\right)}{2}\)
(với n là số tự nhiên khác 0)
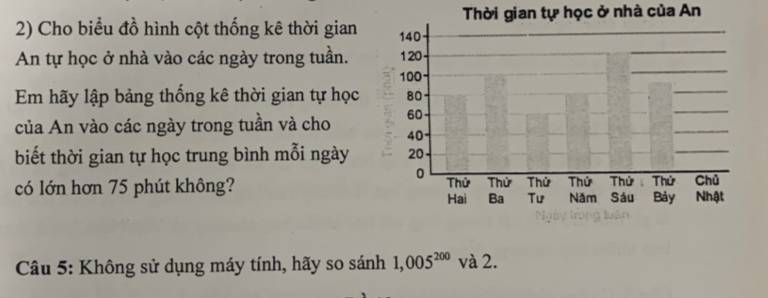
\(\dfrac{2.2020}{1+\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2020}}\)
\(=\dfrac{2.2020}{1+\dfrac{1}{\dfrac{2.3}{2}}+\dfrac{1}{\dfrac{3.4}{2}}+...+\dfrac{1}{\dfrac{2020.2021}{2}}}\)
\(=\dfrac{2.2020}{1+\dfrac{2}{2.3}+\dfrac{2}{3.4}+...+\dfrac{2}{2020.2021}}\)
\(=\dfrac{2.2020}{2.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2020.2021}\right)}\)
\(=\dfrac{2020}{\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\right)}\)
\(=\dfrac{2020}{1-\dfrac{1}{2021}}=\dfrac{2020}{\dfrac{2020}{2021}}=2021\)





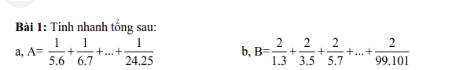

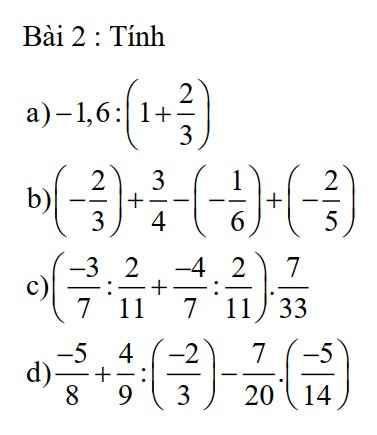 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn