-Tham khảo từ bài GV của mình.
\(A=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(\Rightarrow3A=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(\Rightarrow3A-A=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}-\left(\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\right)\)
\(\Rightarrow2A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
-Đặt \(S=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow3S=3+1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}\)
\(\Rightarrow3S-S=3+1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}-\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\right)\)
\(\Rightarrow2S=3-\dfrac{1}{3^{99}}\)
\(\Rightarrow S=\dfrac{3-\dfrac{1}{3^{99}}}{2}=\dfrac{\dfrac{3^{100}-1}{3^{99}}}{2}=\dfrac{3^{100}-1}{2.3^{99}}\)
\(\Rightarrow2A=\dfrac{3^{100}-1}{2.3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow2A=\dfrac{3\left(3^{100}-1\right)}{2.3^{100}}-\dfrac{200}{2.3^{100}}\)
\(\Rightarrow A=\dfrac{\dfrac{3^{101}-3-200}{2.3^{100}}}{2}=\dfrac{3^{101}-203}{4.3^{100}}\)
\(\dfrac{3}{4}=\dfrac{3^{101}}{4.3^{100}}>\dfrac{3^{101}-203}{4.3^{100}}=A\)
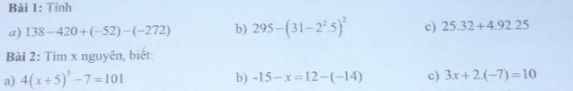giúp tui với 4 giờ tui đi hc rùi
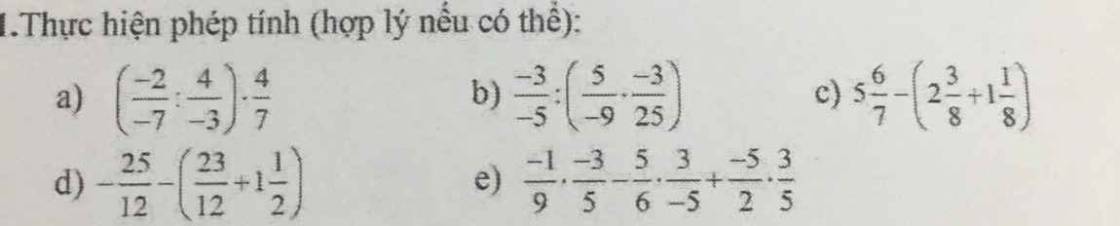
giải giúp tui với ạ sắp đến h đi hc rùi cảm ơn nhìu