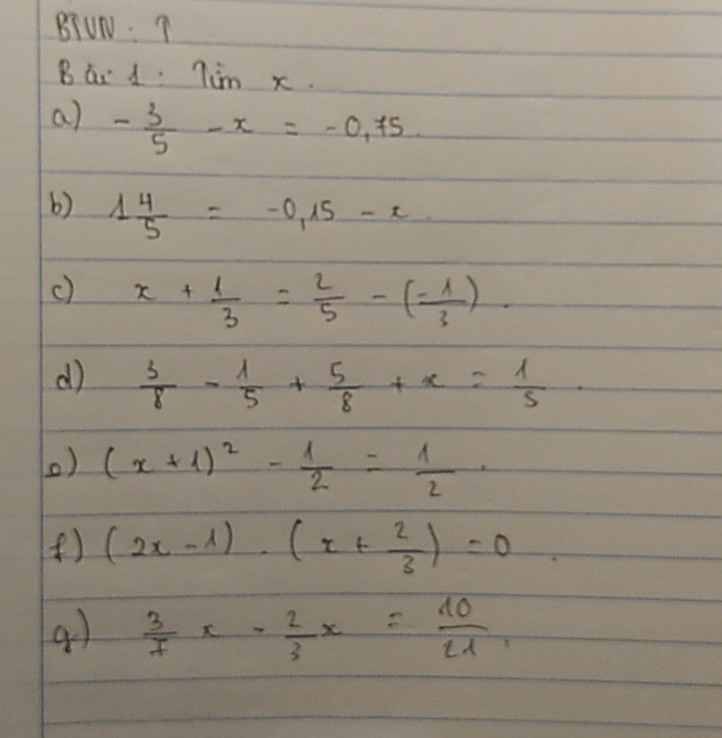b) \(1\dfrac{4}{5}=0,15-x\)
\(\dfrac{9}{5}=0,15-x\)
\(\dfrac{9}{5}-0,15=-x\)
\(-x=\dfrac{33}{20}\Rightarrow x=-\dfrac{33}{20}\)
d) \(\dfrac{3}{8}-\dfrac{1}{5}+\dfrac{5}{8}+x=\dfrac{1}{5}\)
\(\dfrac{4}{5}+x=\dfrac{1}{5}\)
\(x=\dfrac{1}{5}-\dfrac{4}{5}=\Rightarrow x=-\dfrac{3}{5}\)
e) \(\left(x+1\right)^2-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\left(x+1\right)^2=\dfrac{1}{2}+\dfrac{1}{2}=1\)
\(\sqrt{\left(x+1\right)^2}=\sqrt{1}\)
\(x+1=1\Rightarrow x=0\)
f) \(\left(2x-1\right)\left(x+\dfrac{2}{3}\right)=0\)
\(\left[{}\begin{matrix}2x-1=0\\x+\dfrac{2}{3}=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{1}{2};-\dfrac{2}{3}\right\}\).
g) \(\dfrac{3}{7}x-\dfrac{2}{3}x=\dfrac{10}{21}\)
\(x\left(\dfrac{3}{7}-\dfrac{2}{3}\right)=\dfrac{10}{21}\)
\(x\left(-\dfrac{5}{21}\right)=\dfrac{10}{21}\)
\(x=\dfrac{10}{21}:\left(-\dfrac{5}{21}\right)=\dfrac{10}{21}\cdot\left(-\dfrac{21}{5}\right)\)
\(x=-\dfrac{10}{5}=-2\)
`b)`
`1 4/5 = -0,15 -x`
`=> (1xx5+4)/5 = -3/20 -x`
`=> 9/5 = -3/20 -x`
`=> -3/20 -x= 9/5 `
`=> x= -3/20 - 9/5`
`=>x= -3/20 - 36/20`
`=>x= -39/20`