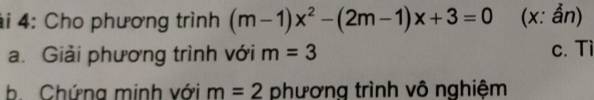\(a,\) Thay \(m=3\) vào pt trên
\(\Leftrightarrow\left(3-1\right)x^2-\left(2.3-1\right)x+3=0\)
\(\Leftrightarrow2x^2-5x+3=0\)
\(\Leftrightarrow2x^2-2x-3x+3=0\)
\(\Leftrightarrow2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=1\end{matrix}\right.\)
\(b,\) Thay \(m=2\) vào pt trên
\(\Leftrightarrow\left(2-1\right)x^2-\left(2.2-1\right)x+3=0\)
\(\Leftrightarrow x^2-3x+3=0\)
\(\Leftrightarrow\) Pt vô nghiệm
Vậy \(S=\varnothing\)
a,
Với `m=3` pt `<=> 2x^2 - 5x + 3 = 0`
`<=> ( 2x +1 )( x-3)=0`
`<=> [(2x+1=0),(x-3=0):}`
`<=> [(x=-1/2),(x=3):}`
Vậy pt có tập nghiệm `S={-1/2;3}`
b,
Với `m=2 ` pt `<=> x^2 - 3x+3=0`
Có `x^2 - 3x+3=x^2-3x+9/4+3/4=(x-3/2)^2+3/4>=3/4\ne0`
Pt vô nghiệm . Vậy `m=2` thì pt vô nghiệm
a) Khi m = 3 ta có: \(2x^2-5x+3=0\)
Ta có: \(\Delta=b^2-4ac=\left(-5\right)^2-4.2.3=1\)
⇒ Phương trình có hai nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)+\sqrt{1}}{2.2}=\dfrac{3}{2}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-5\right)-\sqrt{1}}{2.2}=1\)
b) Khi m = 2 ta có: \(x^2-3x+3=0\)
Ta có: \(\Delta=b^2-4ac=\left(-3\right)^2-4.3=-3\)
Vì △ > 0 nên phương trình vô nghiệm
Vậy khi m = 2 thì phương trình vô nghiệm