a) \(\sqrt{2-x}-\sqrt{x^2-4}=0\) (1)
ĐK: \(\left\{{}\begin{matrix}2-x\ge0\\x^2-4\ge0\end{matrix}\right.< =>\left\{{}\begin{matrix}x\le2\\\left[{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\x\le-2\end{matrix}\right.\)
(1) <=> \(\sqrt{2-x}=\sqrt{x^2-4}\)
<=> 2-x = x2-4
<=>x2 +x-6=0
<=> \(\left[{}\begin{matrix}x=2\left(C\right)\\x=-3\left(C\right)\end{matrix}\right.\)
b) \(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\)(ĐK: \(x\ge5\))
<=> \(2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
<=> x = 9 (TM)

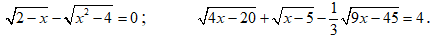




 giúp mk câu c
giúp mk câu c bài 2 tự luận câu c bài hình vs 2 bài cuối với ạ
bài 2 tự luận câu c bài hình vs 2 bài cuối với ạ











 giúp mình câu cuối với
giúp mình câu cuối với