\(d,\left(2x-\dfrac{3}{4}\right)x-1=0\)
\(\Rightarrow2x-\dfrac{3}{4}=0\) hoặc \(x-1=0\)
\(\Rightarrow2x=0+\dfrac{3}{4}\) hoặc \(x=0+1\)
\(\Rightarrow2x=\dfrac{3}{4}\) hoặc \(x=1\)
\(\Rightarrow x=\dfrac{3}{4}:2\) hoặc \(x=1\)
\(\Rightarrow x=\dfrac{3}{8}\) hoặc \(x=1\)
Vậy \(x\in\left\{\dfrac{3}{8};1\right\}\)
d,\(\left(2x-\dfrac{3}{4}\right)x-1\)=0
⇒\(\left(2x-\dfrac{3}{4}\right)x\)=1
⇒\(\left(2x-\dfrac{3}{4}\right)x\) ∈ Ư(1) = {+-1}
TH1:Với x=1
⇒2x-\(\dfrac{3}{4}\)=1 (Do 1.1=1)
⇒2x=1+\(\dfrac{3}{4}\)=\(\dfrac{7}{4}\)
⇒x=\(\dfrac{7}{4}\):2=\(\dfrac{7}{8}\) (không thỏa mãn)
TH2: Với x=-1
⇒\(2x+\dfrac{3}{4}\)=-1 (Do (-1).(-1)=1)
⇒2x=-1-\(\dfrac{3}{4}\)=\(\dfrac{-7}{4}\)
⇒x=\(\dfrac{-7}{4}\):2=\(\dfrac{-7}{8}\) (không thỏa mãn)
Vậy nên phương trình trên vô nghiệm

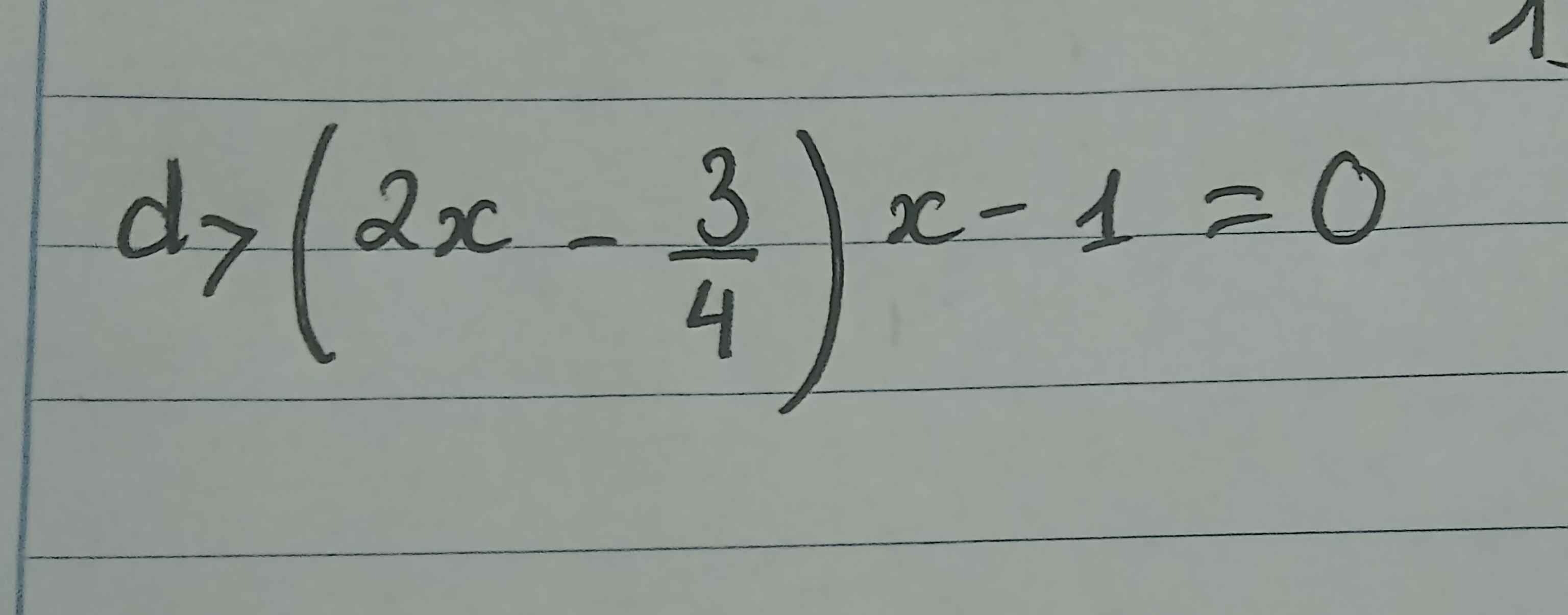























 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước