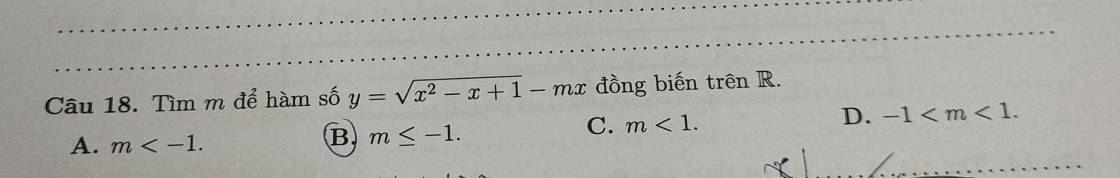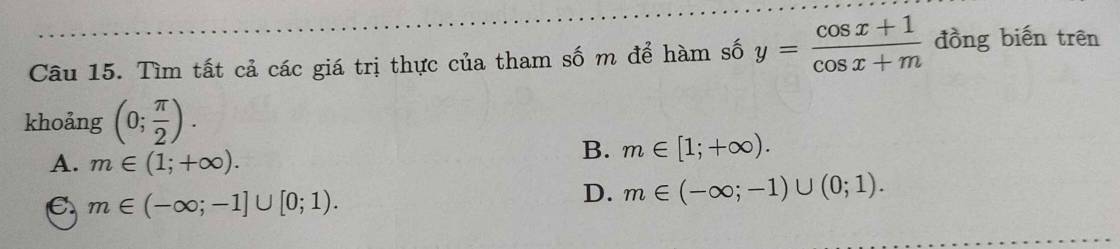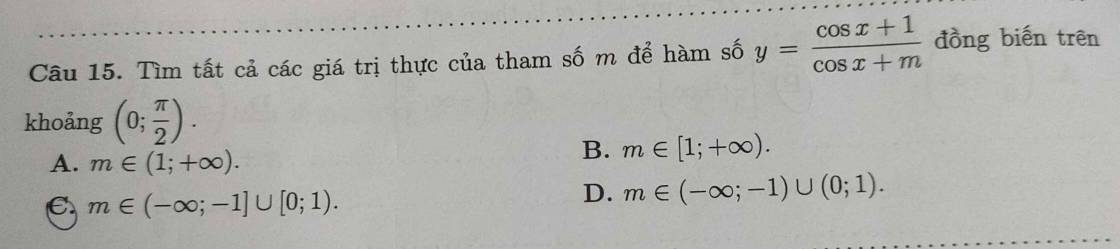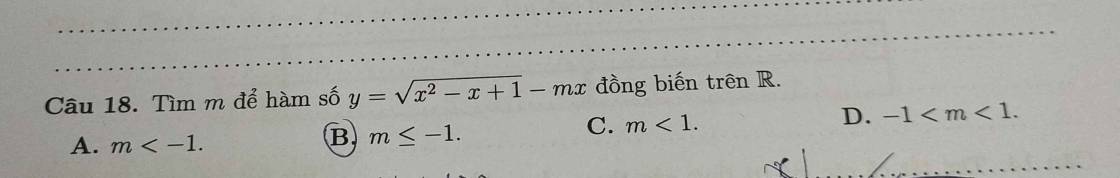20.
Gọi I là trung điểm AB \(\Rightarrow I\left(-1;2;-5\right)\)
\(\overrightarrow{IA}=\left(3;0;4\right)\Rightarrow IA=\sqrt{3^2+0^2+4^2}=5\)
Đường tròn đường kính AB có tâm I và bán kính \(R=IA=5\) nên có pt:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z+5\right)^2=25\)
22.
Từ pt mặt cầu ta thấy (S) có tâm \(I\left(-1;2;-1\right)\) và bán kính \(R=\sqrt{\left(-1\right)^2+2^2+\left(-1\right)^2-0}=\sqrt{6}\)
22.
\(\overrightarrow{AI}=\left(0;1;1\right)\Rightarrow IA=\sqrt{0^2+1^2+1^2}=\sqrt{2}\)
Mặt cầu tâm I đi qua A có bán kính \(R=IA=\sqrt{2}\) nên có pt:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=2\)
23.
Do \(V=\dfrac{4}{3}\pi R^3=36\pi\Rightarrow R=3\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z+4\right)^2=9\)
24.
\(R=d\left(I;\left(\alpha\right)\right)=\dfrac{\left|2.2-2.1-\left(-1\right)+3\right|}{\sqrt{2^2+\left(-2\right)^2+\left(-1\right)^2}}=2\)
25.
\(R=d\left(I;Oyz\right)=\left|x_I\right|=1\)
Phương trình:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=1\)