b) \(5x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{5}\Rightarrow\dfrac{x^2}{16}=\dfrac{y^2}{25}\)
Áp dụng t/c của dãy số bằng nhau, ta có: \(\dfrac{x^2+y^2}{16+25}=\dfrac{164}{41}=4\)
\(\dfrac{x^2}{16}=4\Rightarrow x=8\)
\(\dfrac{y^2}{25}=4\Rightarrow y=10\)
a. $\frac{x}{y}=\frac{3}{7}$
$\Rightarrow \frac{x}{3}=\frac{y}{7}= \frac{2x}{6}=\frac{3y}{21}$
Áp dụng TCDTSBN:
$ \frac{x}{3}=\frac{y}{7}= \frac{2x}{6}=\frac{3y}{21}=\frac{2x-3y}{6-21}=\frac{24}{-15}=\frac{-8}{5}$
$\Rightarrow x=3.\frac{-8}{5}=\frac{-24}{5}; y=7.\frac{-8}{5}=\frac{-56}{5}$
b.
$5x=4y\Leftrightarrow \frac{x}{4}=\frac{y}{5}=t$
$\Rightarrow x=4t; y=5t$
Khi đó:
$x^2+y^2=(4t)^2+(5t)^2=164$
$\Leftrightarrow 41t^2=164$
$\Leftrihgtarrow t^2=4\Rightarrow t=\pm 2$
Nếu $t=2$ thì $x=4t=8; y=5t=10$
Nếu $t=-2$ thì $x=4t=-8; y=5t=-10$
c.
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{2}=\frac{y}{3}=\frac{z}{6}=\frac{x-y+z}{2-3+6}=\frac{25}{5}=5$
$\Rightarrow x=2.5=10; y=3.5=15; z=6.5=30$
d. Áp dụng TCDTSBN:
$\frac{x}{7}=\frac{y}{5}=\frac{z}{2}=\frac{2z}{4}=\frac{2z-x}{4-7}=\frac{-9}{-3}=3$
$\Rightarrow x=7.3=21; y=5.3=15; z=2.3=6$
e. Áp dụng TCDTSBN:
$2x=3y=4z$
$\Rightarrow \frac{x}{\frac{1}{2}}=\frac{y}{\frac{1}{3}}=\frac{z}{\frac{1}{4}}=\frac{x-z}{\frac{1}{2}-\frac{1}{4}}=\frac{30}{\frac{1}{4}}=120$
$\Rightarrow x=\frac{1}{2}.120=60; y=\frac{1}{3}.120=40; z=\frac{1}{4}.120=30$

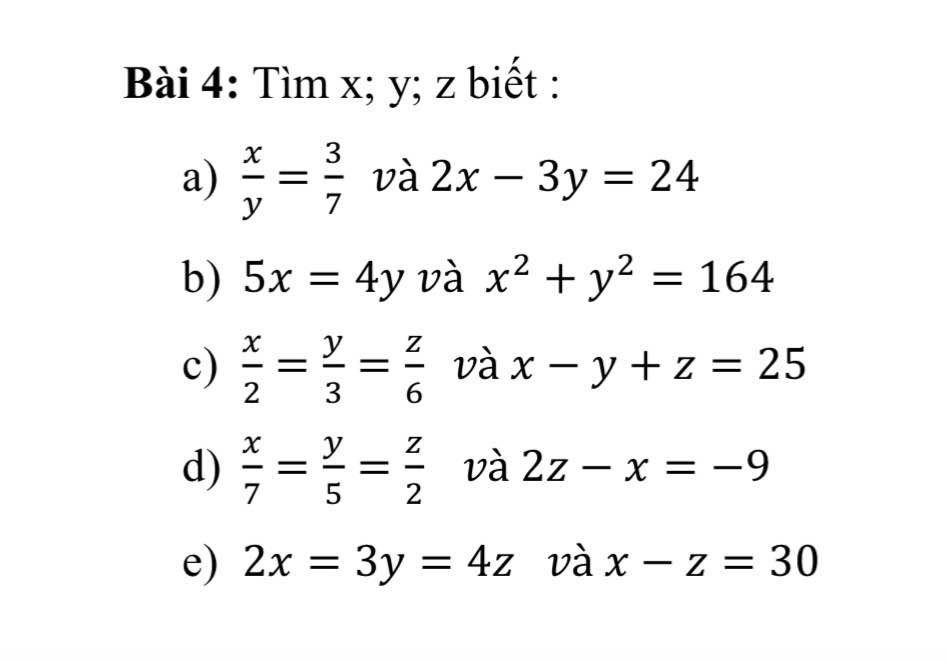






















 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước