\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)

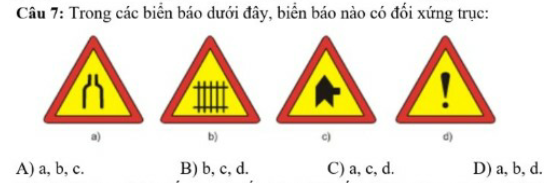
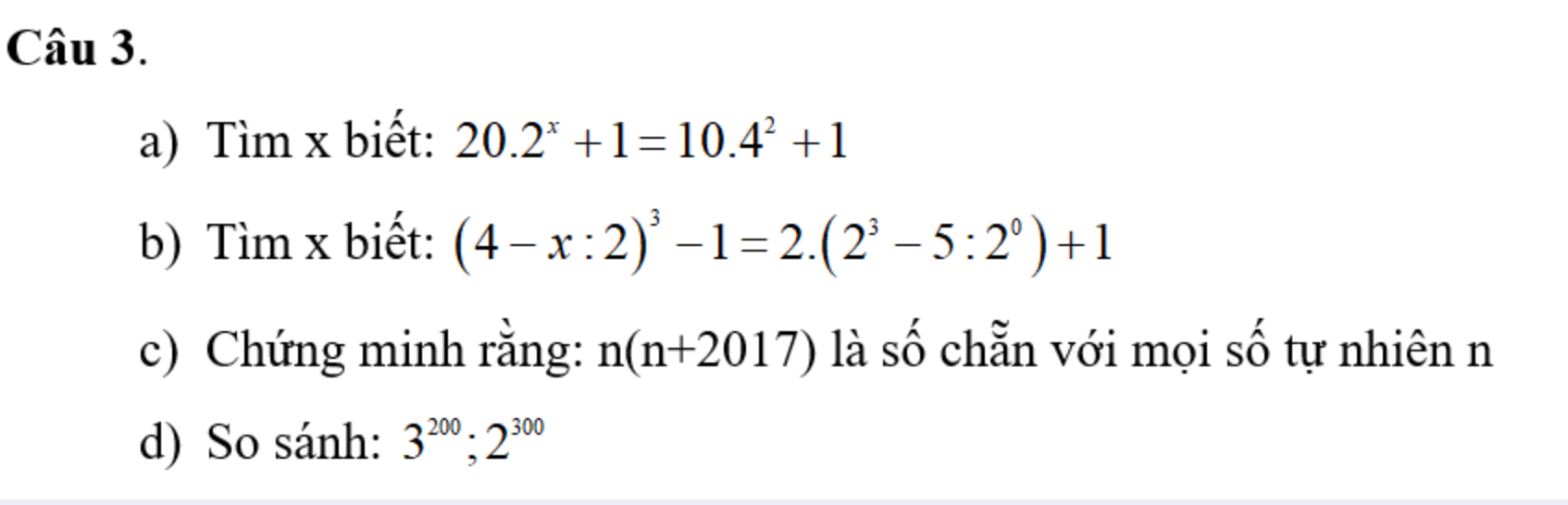 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi