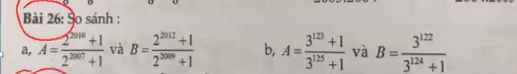\(\dfrac{x+1}{2021}+\dfrac{x+2}{2020}+\dfrac{x+3}{2019}=-3\)
\(\Leftrightarrow\left(\dfrac{x+1}{2021}+1\right)+\left(\dfrac{x+2}{2020}+1\right)+\left(\dfrac{x+3}{2019}+1\right)=0\)
\(\Leftrightarrow\dfrac{x+1+2021}{2021}+\dfrac{x+2+2020}{2020}+\dfrac{x+3+2019}{2019}=0\)
\(\Leftrightarrow\dfrac{x+2022}{2021}+\dfrac{x+2022}{2020}+\dfrac{x+2022}{2019}=0\)
\(\Leftrightarrow\left(x+2022\right)\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2019}\right)=0\)
\(\Leftrightarrow x+2022=0\)
\(\Leftrightarrow x=-2022\)
Vậy \(S=\left\{-2022\right\}\)
`[x+1]/2021+[x+2]/2020+[x+3]/2019=-3`
`=>[x+1]/2021+1+[x+2]/2020+1+[x+3]/2019+1=-3+1+1+1`
`=>[x+1+2021]/2021+[x+2+2020]/2020+[x+3+2019]/2019=0`
`=>[x+2022]/2021+[x+2022]/2020+[x+2022]/2019=0`
`=>(x+2022)(1/2021+1/2020+1/2019)=0`
Mà `1/2021+1/2020+1/2019 \ne 0`
`=>x+2022=0`
`=>x=-2022`
Vậy `x=-2022`
mình cảm ơn các bạn ạ
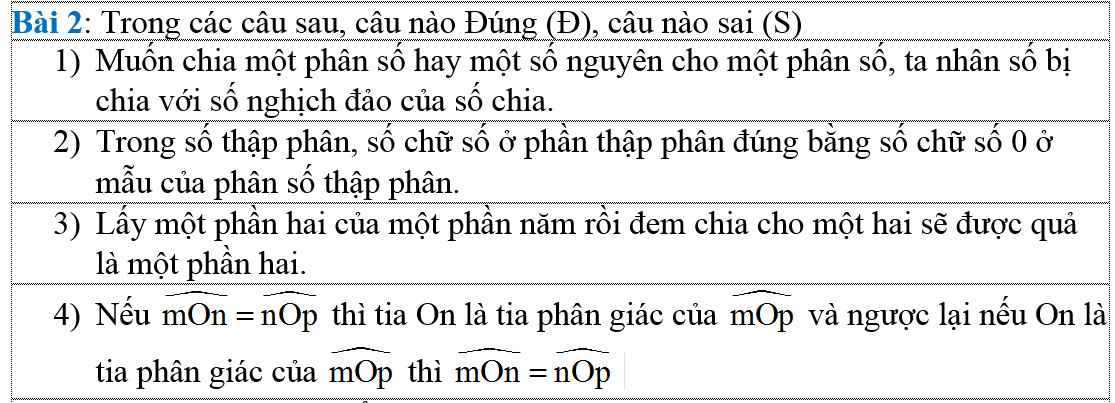
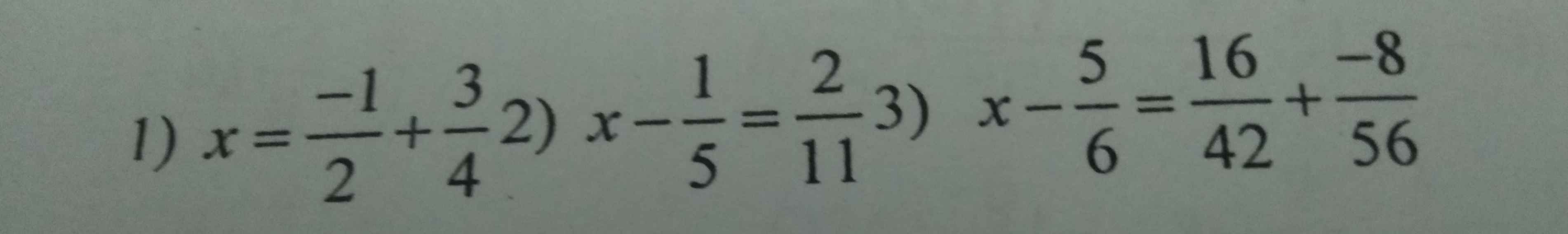
các bạn giúp mình nhnh với ạ , cảm ơn các bạn nhiều
