Question

Giúp mình với ạ

Answer 1

a, Theo tc 2 tt cắt nhau: \(AC=CM;BD=DM\)

\(\Rightarrow AC+BD=CM+MD=CD\)

b, \(\widehat{CAO}=\widehat{CMO}=90^0;CO\text{ chung};AC=CM\)

\(\Rightarrow\Delta CAO=\Delta CMO\left(ch-cgv\right)\\ \Rightarrow\widehat{AOC}=\widehat{COM}=\dfrac{1}{2}\widehat{AOM}\)

Cmtt \(\Rightarrow\Delta BOD=\Delta MOD\left(ch-cgv\right)\)

\(\Rightarrow\widehat{BOD}=\widehat{MOD}=\dfrac{1}{2}\widehat{BOM}\)

\(\Rightarrow\widehat{COD}=\widehat{COM}+\widehat{MOD}=\dfrac{1}{2}\left(\widehat{AOM}+\widehat{BOM}\right)=\dfrac{1}{2}\cdot180^0=90^0\\ \Rightarrow\Delta COD\text{ vuông tại }O\)

c, Áp dụng HTL: \(AC\cdot BD=MC\cdot MD=OC^2=OA^2\left(\text{cùng là bán kính}\right)\)

\(\Rightarrow AC\cdot BD=OA^2=\left(\dfrac{AB}{2}\right)^2=\dfrac{AB^2}{4}\)

Answer 2

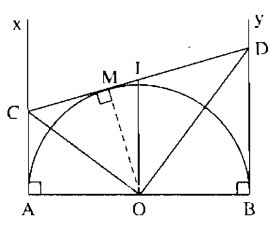 a) Ta có 2 tiếp tuyến Ax và CM cắt nhau tại C 

⇒C thuộc đường trung trực AM⇒  CA=CM  

Tượng tự có    DB  = DM   

Ta có CD= CM+MD = CA+BD

b) Ta có CO là đường trung trực của△ AMO

⇒CO là đường phân giác △ AMO   (1)

tương tự có DO là đường phân giác △ BOM   (2)

Từ 1,2 suy ra CO ⊥ DO ( tính chất hai góc kề bù)

⇒ △ COD vuông tại O

c)  Ta có COA^+COD^+BOD^=180

⇒ COA^+BOD^=180-90=90

mà COA^+ ACO^=90 ⇒BOD^= ACO^

Xét △ACO và  △ BOD  đồng dạng do có: BOD^= ACO^ và OAC^=DBO^

⇒AC/AO=OB/BD

⇒AC.BD=AO.BO=1/2AB.1/2AB=1/4AB²